Introduction
This document gathers explanations on the solutions of the Euler Project exercises. Each exercise has its own part, which can be discovered in the table of contents. You can find the source code of every solution as well as the source code of my mdBook on my Github: TurtleSmoke Project Euler.
Project Euler
What is Project Euler?
Project Euler is a series of challenging mathematical/computer programming problems that will require more than just mathematical insights to solve. Although mathematics will help you arrive at elegant and efficient methods, the use of a computer and programming skills will be required to solve most problems.
The motivation for starting Project Euler, and its continuation, is to provide a platform for the inquiring mind to delve into unfamiliar areas and learn new concepts in a fun and recreational context.
Who are the problems aimed at?
The intended audience include students for whom the basic curriculum is not feeding their hunger to learn, adults whose background was not primarily mathematics but had an interest in things mathematical, and professionals who want to keep their problem solving and mathematics on the cutting edge.
Currently we have 1036139 registered members who have solved at least one problem, representing 220 locations throughout the world, and collectively using 108 different programming langues to solve the problems.
Can anyone solve the problems?
The problems range in difficulty and for many the experience is inductive chain learning. That is, by solving one problem it will expose you to a new concept that allows you to undertake a previously inaccessible problem. So the determined participant will slowly but surely work his/her way through every problem.
What next?
In order to track your progress it is necessary to setup an account and have Cookies enabled.
If you already have an account, then Sign In. Otherwise, please Register – it's completely free! However, as the problems are challenging, then you may wish to view the Problems before registering.
Project Euler exists to encourage, challenge, and develop the skills and enjoyment of anyone with an interest in the fascinating world of mathematics.
Multiples of 3 or 5
If we list all the natural numbers below \( 10 \) that are multiples of \( 3 \) or \( 5 \), we get \( 3 \), \( 5 \), \( 6 \) and \( 9 \). The sum of these multiples is \( 23 \).
Find the sum of all the multiples of \( 3 \) or \( 5 \) below \( 1000 \).
Brute force
The first problem is actually quite easy, the naive solution is to iterate over each number between 0 and 1000 and check those that are multiples of 3 or 5.
From solution1.py:
def sum_of_three_and_five(limit=1000):
return sum(i for i in range(limit) if i % 3 == 0 or i % 5 == 0)
Three by three
The Brute force is actually quite slow, at least it would be if the limit was greater than 1000. Since only multiples of 3 and 5 are useful, iterating 3 by 3 and then 5 by 5 will be faster. We have to be careful with the multiples of 3 and 5 because they will be counted twice. So we have to subtract them from the result.
From solution2.py:
def sum_of_three_and_five(limit=1000):
sum_3 = sum(i for i in range(0, limit, 3) if i % 3 == 0)
sum_5 = sum(i for i in range(0, limit, 5) if i % 5 == 0)
sum_15 = sum(i for i in range(0, limit, 15) if i % 15 == 0)
return sum_3 + sum_5 - sum_15
Summing everything
The Three by three solution is quite interesting because it reduces the problem into smaller parts. For example, the sum of multiples of three is the following:
\[ 3 + 6 + 9 + 12 + 15 + ... \] \[ 3 * ( 1 + 2 + 3 + 4 + 5 ...) \] \[ 3 * \sum_{i=0}^{\lfloor\frac{1000}{3}\rfloor} x_i \]
It is the sum of an arithmetic sequences, which is equal to:
\[ \frac{n*(n+1)}{2} \]
The Three by three solution can be reduced to:
\[ 3 * \frac{\lfloor\frac{999}{3}\rfloor * (\lfloor\frac{999}{3}\rfloor + 1)}{2} +5 * \frac{\lfloor\frac{999}{5}\rfloor * (\lfloor\frac{999}{5}\rfloor + 1)}{2} -15 * \frac{\lfloor\frac{999}{15}\rfloor * (\lfloor\frac{999}{15}\rfloor + 1)}{2} \]
Note that the limit is 999 because 1000 should not be included.
From solution3.py:
def sum_of_three_and_five(limit=999):
limit_3 = limit // 3
limit_5 = limit // 5
limit_15 = limit // 15
sum_3 = 3 * (limit_3 * (limit_3 + 1) // 2)
sum_5 = 5 * (limit_5 * (limit_5 + 1) // 2)
sum_15 = 15 * (limit_15 * (limit_15 + 1) // 2)
return sum_3 + sum_5 - sum_15
Solution
233168
Even Fibonacci numbers
Each new term in the Fibonacci sequence is generated by adding the previous two terms. By starting with \( 1 \) and \( 2 \), the first \( 10 \) terms will be:
\[ 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... \]
By considering the terms in the Fibonacci sequence whose values do not exceed four million, find the sum of the even-valued terms.
Brute force
The Fibonacci numbers form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1.
The sum of all even numbers in the Fibonacci sequence less than 4 million can be calculated quite easily by iterating over the sequence until the threshold is reached by adding each even number to the result.
From solution1.py:
def sum_of_even_fibonacci_numbers(limit=4000000):
f0 = 1
f1 = 2
res = 0
while f0 < limit:
if f0 % 2 == 0:
res += f0
f0, f1 = f1, f0 + f1
return res
Fibonacci recurrence
If we take a look at the Fibonacci series:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ...
Since our only concern is the parity of the numbers, with O being odd and E even:
E, O, O, E, O, O, E, O, O, E, O, O, E, O, O, E, ...
It seems that every third number of the series is even, let's try to prove it properly.
\[ \begin{gather} If\ n=0\ then\ F_{0}=0\ is\ even\\\\ Assuming\ that\ F_ {3n} \ is\ even.\\ \\ F_{3( n+1)} =F_{3n+2} +F_{3n+1} =( F_{3n+1} +F_{3n}) +F_{3n+1} =2F_{3n+1} +F_ {3n}\\ \\ Since\ F_{3n} \ is\ even\ and\ 2F_{3n+1} \ is\ also\ even,\ we\ have\ F_{3( n+1)} \ even\\ because\ it\ is\ the\ sum\ of\ two\ even\ numbers. \end{gather} \]
This mean that the series of even Fibonacci number is:
\[ \begin {gather} E_{n} = F_{3n}\\ E_{n+2} = F_{3n+6} = F_{3n+5} + F_ {3n+4}\\ E_{n+2} = (F_{3n+4} + F_{3n+3}) + (F_{3n+3} + F_{3n+2})\\ E_{n+2} = (F_{3n+3} + F_{3n+2} + F_{3n+3}) + (F_{3n+3} + F_{3n+1} + F_{3n})\\ E_{n+2} = 3F_{3n+3} + (F_{3n+2} + F_{3n+1}) + F_{3n}\\ E_{n+2} = 4F_{3(n+1)} + F_{3n}\\ E_{n+2} = 4E_{n+1} + E_{n}\\ \end{gather} \]
Which result int the following recurrence relation:
\[ E_{n} = 4E_ {n-1} + E_{n-2} \]
We are searching for:
\[ \sum_{k=1}^ {n}E_k \]
This can be simplified as follows:
\[ \begin{align} \sum_{k=1}^{n}E_ {k+1} &= \sum_{k=1}^{n}4E_{k} + \sum_{k=1} ^{n}E_{k-1}\\ \sum_{k=1}^{n}E_{k}&= \frac{1}{4}(\sum_{k=1}^{n}E_{k+1} - \sum_{k=1}^{n}E_{k-1})\\ &= \frac{1}{4}(\sum_{k=2}^{n+1}E_{k} - \sum_{k=0}^{n-1}E_{k})\\ &= \frac{1}{4}(E_{n+1} + E_{n} - E_1 - E_0)\\ &= \frac{1}{4}(E_{n+1} + E_{n} - 2)\\ \end{align} \]
The result can be calculated by iterating until \( E_{n+1} \) is greater than the limit, so that \( E_n \) is less than the limit, then apply the previous function.
From solution2.py:
def sum_of_even_fibonacci_numbers(limit=4000000):
e0 = 0
e1 = 2
while e1 < limit:
e0, e1 = e1, 4 * e1 + e0
return (e1 + e0 - 2) // 4
Fibonacci and the golden ratio
Although the number of iterations of the second solution is lower than that of the first solution, it is possible to do better:
\[ \begin{align} \frac{1}{4}(E_{n+1} + E_{n} - 2) &= \frac{1}{4}(F_{3(n+1)} + F_{3n} - 2)\\ &= \frac{1}{4}(F_{3n+2} + F_{3n+1} + F_{3n} - 2)\\ &= \frac{1}{4}(2F_{3n+2} - 2)\\ &= \frac{1}{2}(F_{3n+2} - 1)\\ \end{align} \]
This does not really change the problem, since we still need to iterate until \( F_{3n} \) reach the limit and then compute \(\frac{1}{2}(F_ {3n+2} - 1)\).
Actually, the Fibonacci numbers can be approximated with the following equation:
\[ F_{n} = \frac{\varphi^{n} - (-\varphi)^{-n}}{\sqrt{5}} \]
where \( \varphi = \frac{1+\sqrt{5}}{2} \) is the golden ratio.
\( -(-\varphi)^{-n} \) can be ignored for large numbers which gives the equation:
\[ F_{n} = \frac{\varphi^{n}}{\sqrt{5}} \]
The limit is the n-th Fibonacci number such that:
\[ \begin{align} F_{n} &\leqslant M\\ \frac{\varphi ^{n}}{\sqrt{5}} &\leqslant M\\ \varphi ^{n} &\leqslant \sqrt{5} M\\ n\log( \varphi ) &\leqslant \log\left(\sqrt{5} M\right)\\ n &\leqslant \left\lfloor \frac{\log\left(\sqrt{5} M\right)}{\log( \varphi )} \right\rfloor \end{align} \]
The result can be computed with \(\frac{1}{2}(F_{n+2} - 1) \) where \( n = \left\lfloor \frac{\log\left(\sqrt{5} M\right)}{\log( \varphi )} \right\rfloor \):
From solution3.py:
def sum_of_even_fibonacci_numbers(limit=4000000):
golden_ratio = (1 + sqrt(5)) / 2
n = floor(log(sqrt(5) * limit) / log(golden_ratio))
fn = round((golden_ratio ** (n + 2)) / sqrt(5))
return (fn - 1) // 2
Solution
4613732
Largest prime factor
The prime factors of \( 13195 \) are \( 5 \), \( 7 \), \( 13 \) and \( 29 \).
What is the largest prime factor of the number \( 600851475143 \) ?
Brute force
\( i \) is a factor of \( n \) if \( n\ \equiv\ 0\ [i] \), in our case it is enough to iterate over each number. When a factor is found, we simply divide \( n \) by that factor and continue as long as \( n \) is greater than one. When \( n \) is equal to one, we simply return the current factor which is also the largest.
From solution1.py:
def largest_prime_factor(n=600851475143):
res = 2
while n != 1:
if n % res == 0:
n //= res
else:
res += 1
return res
Two by Two
Since all primes except 2 are odd and in our case 2 is not a factor of 600851475143, we can start with 3 and iterate two by two, which is not a great improvement, but this problem has no interesting solution anyway.
From solution2.py:
def largest_prime_factor(n=600851475143):
res = 3
while n != 1:
if n % res == 0:
n //= res
else:
res += 2
return res
Solution
6857
Largest palindrome product
A palindromic number reads the same both ways. The largest palindrome made from the product of two \( 2 \)-digit numbers is \( 9009=91×99 \).
Find the largest palindrome made from the product of two \( 3 \)-digit numbers.
Brute force
We are searching the largest palindrome made from the product of two 3-digit numbers. Firstly, it is necessary to know when a number is a palindrome. This can be done easily using python iteration.
From solution1.py:
def is_palindrome(n):
return str(n) == str(n)[::-1]
A better solution exists using modulus and division, but performance is not the goal here.
The range of 3-digit numbers is \( [100; 999] \), the naive solution will consist in simply iterate over each number and check which product is the largest palindrome. A little trick: if \( 100 * 200 \) does not work, \( 200 * 100 \) won't work either, so the second loop starts from the current number of the first one.
From solution1.py:
def largest_palindrome_product():
res = 0
for x in range(100, 1000):
for y in range(x, 1000):
if x * y > res and is_palindrome(x * y):
res = x * y
return res
Factorisation is the key
We know that the researched number is larger than \( 100*100 = 10000 \) and smaller than \( 999*999 = 998001 \). So it must be of the form \( abcba \) or \( abccba \). Let's assume it is of the form \( abccba \), if it does not work, we'll try with \( abcba \).
\( abccba = 10001a + 10010b + 1100c = 11(9091a + 910b + 100c) \) which means that the palindrome must be divisible by 11. Since 11 is prime, either \( 100001a \), \( 10010b \) or \( 1100c \) is a multiple of 11, which is why the iteration can be done 11 by 11.
From solution2.py:
def largest_palindrome_product():
res = 0
for x in range(110, 1000, 11):
for y in range(x, 1000):
if x * y > res and is_palindrome(x * y):
res = x * y
return res
We went from 405450 iterations with the Brute force to 36450 iterations !
With pen and paper
In Factorisation is the key, we assume that the number was of the form \( abccba \). Since it is the factor of two 3-digit number, we have :
\[ \begin{align} abccba &= (100a + 10b + c)(100d + 10e + f)\\ &= 10000ad + 1000(bd + ae) + 100(cd + be + af) + 10(ce + bf) + cf \end{align} \]
Assuming the first digit is 9, then \( cf \) must be equal to 9 as well.
The only ways to make the last digit nine are:
\[ 1 * 9\\ 3 * 3\\ 7 * 7 \]
Thus, both number must start with 9 and end with either 1, 3, 7 or 9. We also know that \( 100a + 10b + c \) or \( 100d + 10e + f \) is divisible by 11. The only numbers divisible by 11 and ending with 1, 3, 7 or 9 in the \( [900; 999] \) are :
\[ 913\\ 957\\ 979 \]
This give us:
\[ \text{a = 9}\\ \text{b = 1, 5 or 7}\\ \text{c = 3, 7 or 9}\\ \]
Resulting in the numbers:
\[ (900 + 10 + 3)(900 + 10e + 3) = 824439 + 9130x\\ (900 + 50 + 7)(900 + 10e + 7) = 867999 + 9570x\\ (900 + 70 + 9)(900 + 10e + 1) = 882079 + 9790x \]
The first number implies that \( e \) is equal to 9 because if \( e \) was equal to 8, then \(824439 * 9130 * 8 = 897479 \) would not start with 9. With \( e = 9 \) we have \( 913 * 993 \) which is the correct answer. Both \( (900 + 50 + 7)(900 + 10e + 7) \) and \( (900 + 70 + 9)(900 + 10e + 1) \) give smaller palindrome.
Solution
906609
Smallest multiple
\( 2520 \) is the smallest number that can be divided by each of the numbers from \( 1 \) to \( 10 \) without any remainder.
What is the smallest positive number that is evenly divisible by all of the numbers from \( 1 \) to \( 20 \)?
Brute force
As always, the brute force solution is quite simple, first determine if a number is evenly divisible by all numbers from 1 to 20.
From solution1.py:
def is_evenly_divisible(n):
for i in range(1, 21):
if n % i != 0:
return False
return True
Then iterate until you find a solution.
From solution1.py:
def smallest_multiple():
i = 1
while not is_evenly_divisible(i):
i += 1
return i
Prime factorization
The Brute force is actually very slow. A better solution can be found using prime factorization. The key is to understand that when \( x \) divides \( y \) evenly, it is because the prime factors of \( x\) are contained in \( y \). For example, \( 20 = 2^2 * 5 \) which means that a number divisible by 20 is also divisible by 2, 4 and 5.
Calculating the prime factorization of each number from 1 to 20 give us:
\[\begin{align} 20 &= 2^2 * 5\\ 19 &= 19\\ 18 &= 2 * 3^2\\ 17 &= 17\\ 16 &= 2^4\\ 15 &= 3 * 5\\ 14 &= 2 * 7\\ 13 &= 13\\ 12 &= 2^2 * 3\\ 11 &= 11\\ \end{align} \]
We can stop here, because 10 is included in 20, 9 in 18, 8 in 16, 7 in 14, 6 in 12, 5 in 20, 4 in 20, 3 in 18, 2 in 20 and 1 in 20.
It gives us the answer: \( 2^4 * 3^2 * 5 * 7 * 11 * 13 * 17 * 19 = 232792560 \).
Least common multiple
Actually, the problem is to find the least common multiple which is:
\[ LCT(1, 2, ..., N) \]
To find the \( LCT \) of \( 1 \) through \( N \), we need all the primes \( \leqslant N \). For each prime, we need its maximum power that won't exceed \( N \). Which can be done easily using logarithms:
\[ \begin{align} p^{k} &\leqslant N\\ k\log( p) &\leqslant \log( N)\\ k&=\left\lfloor \frac{\log( N)}{\log( p)}\right\rfloor\\ \end{align} \]
So the \( LCT \) of \( 1 \) through \( N \) is:
\[ \prod p^{\left\lfloor \frac{\log(N)}{\log(p)} \right\rfloor } \]
We also know that it's pointless to search the maximum power of primes greater than \( \sqrt{n} \) because it will always be 1.
From solution3.py:
def smallest_multiple(n=20):
# Returns a list of all primes <= n
primes = sieve.primerange(n + 1)
sqrt_n, log_n = sqrt(n), log(n)
res = 1
for p in primes:
if p < sqrt_n:
res *= p ** (floor(log_n / log(p)))
else:
res *= p
return res
Solution
232792560
Sum square difference
The sum of the squares of the first ten natural numbers is,
\[ 1^2 + 2^2 + ... + 10^2 = 385 \]
The square of the sum of the first ten natural numbers is,
\[ (1 + 2 + ... + 10)^2 = 55^2 = 3025 \]
Hence the difference between the sum of the squares of the first ten natural numbers and the square of the sum is \( 3025-385=2640 \).
Find the difference between the sum of the squares of the first one hundred natural numbers and the square of the sum.
Brute force
Finding the difference between the sum of the squares and the square of the sum required two steps:
Find the sum of the squares:
From solution1.py:
def sum_of_squares(n):
return sum(i**2 for i in range(1, n + 1))
And the square of the sum:
From solution1.py:
def square_of_sum(n):
return sum(i for i in range(1, n + 1)) ** 2
Finally, just subtract the square of the sum by the sum of the squares:
From solution1.py:
def sum_square_difference(n=100):
return square_of_sum(n) - sum_of_squares(n)
Summation formula
We learned in Problem 1: Multiples of 3 and 5 that:
\[ \sum{k} = \frac{n(n+1)}{2} \]
This gives the following formula for the square of the sum:
\[ (1+2+...+10)^2 = \left(\sum{k}\right)^2 = \left(\frac{n(n+1)}{2}\right)^2 = \frac{n^2 (n+1)^2}{4} \]
The sum of the squares can be found using the formula:
\[ \sum{k^2} = \frac{n(n+1)(2n+1)}{6} \]
There are many demonstrations to prove this equation, let's just look at one of them:
\[ \begin{align} ( k-1)^{3} &=k^{3} -3k^{2} +3k-1\\ k^{3} -( k-1)^{3} &=3k^{2} -3k+1\\ \sum _{k=1}^{n}\left( k^{3} -( k-1)^{3}\right) &=\sum _{k=1}^{n} 3k^{2} -3k+1 \\ \sum _{k=1}^{n} k^{3} -\sum _{k=1}^{n}( k-1)^{3} &=3\sum _{k=1}^{n} k^{2} -3\sum _{k=1}^{n} k+\sum _{k=1}^{n} 1\\ \sum _{k=1}^{n} k^{3} -\sum _{k=0}^{n-1} k^{3} &=3\sum _{k=1}^{n} k^{2} -3\frac{n( n+1)}{2} +n\\ n^{3} &=3\sum _{k=1}^{n} k^{2} -3\frac{n( n+1)}{2} +n\\ \sum _{k=1}^{n} k^{2} &=\frac{1}{3} n^{3} +\frac{n( n+1)}{2} -\frac{1}{3} n\\ \sum _{k=1}^{n} k^{2} &=\frac{n( n+1)( 2n+1)}{6} \end{align} \]
The solution can be found in constant time with these two equations:
\[ \frac{n^2(n+1)^2}{4} - \frac{n(n+1)(2n+1)}{6} = \frac{3n^4+2n^3-3n^2-2n}{12} \]
From solution2.py:
def sum_square_difference(n=100):
return (3 * n**4 + 2 * n**3 - 3 * n**2 - 2 * n) // 12
Solution
25164150
10001st prime
By listing the first six prime numbers: \( 2 \), \( 3 \), \( 5 \), \( 7 \), \( 11 \), and \( 13 \), we can see that the \( 6 \)th prime is \( 13 \).
What is the \( 10001 \)st prime number?
Brute force
A well known and fast way to generate primes is the Sieve of Eratosthenes. The only problem is that we need an upper bound, which is not the case here since we don't know the size of the 10001st prime.
We will have to test the primality of each number, if it is prime, then we store it, otherwise we continue with the next number until the list of prime numbers that we stored contains 10001 elements. The last one being the answer.
To determine the primality of a number, we can check if one of the preceding primes can divide it, if not, the number is prime.
Since even number can not be prime, we can go two by two just like the Two by Two solution of Problem 3: Largest prime factor.
From solution1.py:
def n_th_prime(n=10001):
i = 3
primes = [2]
while len(primes) < n:
if all(i % p != 0 for p in primes): # No divisor in the previous prime.
primes.append(i)
i += 2
return primes[-1]
Almost six by six
Actually, it is possible to speed up a little the previous program knowing that every prime \( n > 3 \) is of the form :
\[ 6k+1 \text{ or } 6k-1 \]
Let's try to persuade ourselves that this is true. All prime numbers are of the form:
\[ 6k - 1\\ 6k\\ 6k+1\\ 6k+2\\ 6k+3\\ 6k+4\\ \]
Nothing amazing, but as we are looking for prime number, we can remove some of them :
\( 6k \), \( 6k + 2 \) and \( 6k + 4 \) are even number, so they cannot be prime.
\( 6k + 3 = 3(3k + 1) \) which is divisible by 3 and thus not prime (except 3).
Which let us with: \( 6k + 1 \) and \( 6k - 1 \).
Thus, we can rewrite the old program to check only those numbers.
From solution2.py:
def n_th_prime(n=10001):
i = 1
primes = [2, 3]
while len(primes) < n:
if all((6 * i - 1) % p != 0 for p in primes):
primes.append(6 * i - 1)
if all((6 * i + 1) % p != 0 for p in primes):
primes.append(6 * i + 1)
i += 1
return primes[n - 1]
Prime number theorem
As I said in the Brute force solution, the fasted way to generate primes is the sieve of eratosthenes, but it requires an upper bound. We can not find the exact upper bound, but we can have a good approximation using the Prime number theorem:
\[ \pi(N) \sim \frac{N}{\log(N)} \]
Where \( \pi(N) \) is the prime-counting function .
This function give the number of primes \( M \) less than or equal to \( N \), in our case we want to determine \( N \) knowing \( M \). Which give us another formula:
\[ \begin{align} \frac{N}{\log(N)} &\leqslant M\\ \frac{\log(N)}{N} &\leqslant \frac{1}{M}\\ -\frac{\log(N)}{N} &\leqslant -\frac{1}{M}\\ -\frac{\log(N)}{e^{\log(N)}} &\leqslant -\frac{1}{M}\\ -\log(N)e^{-\log(N)} &\leqslant -\frac{1}{M} \end{align} \]
The Lambert \( W \) function says that \( we^w = z \Leftrightarrow w = \mathit{W}_{k}(z) \). This give us:
\[ \begin{align} -\log( N) e^{-\log( N)} &\leqslant -\frac{1}{M}\\ -\log( N) &\leqslant W_{k}\left( -\frac{1}{M}\right)\\ N &\leqslant e^{-W_{k}\left( -\frac{1}{M}\right)} \end{align} \]
The solutions of Lambert's \( W \) function with real number can be found with ony two branches: \( W_0 \) and \( W_{-1} \) suffice.
For real number \( z \) and \( w \) the equation \( we^w = z \) can be solved for \( w \) only if \( w \geqslant -\frac{1}{e} \). if \( z \geqslant 0 \) we get \( w = W_0(z) \) and the two values \( w = W_0(z) \) and \( w = W_{-1}(z) \) if \( -\frac{1}{e} \leqslant w < 0 \).
We have \( w = -\log(N) \) so we are in the second case. We need to determine which of \(W_0(z) \) and \( W_{-1}(z) \) is the right formula.
The branch 0 converge to 1 when \( z \) converge to 0. Actually, for \( M > 3 \) we have \( \lceil W_k(-\frac{1}{M}) \rceil = 1\). It implies that the good branch is -1.
We can actually build the sieve of eratosthenes with the upper bound \( e^ {-W_ {-1}(-\frac{1}{M})} \). Lambert's \( W \) function cannot be expressed in terms of elementary functions, so the formula cannot be simplified. The value of Lambert's \( W \) function requires an iterative method to be found, as this is quite a difficult problem we will use the lambertw from scipy to determine our upper bound.
From solution3.py:
def n_th_prime(n=10001):
if n < 3:
return [2, 3][n - 1]
limit_pi_1 = ceil(exp(-lambertw(-1 / n, -1).real))
primes = sieve.primerange(limit_pi_1 + 1)
return next(islice(primes, n - 1, n))
Note that sieve.primerange returns a generator, so we use slice to get the
n-th element.
When \( N < 3 \), we have \( -\log(N) \geqslant -\frac{1}{e} \) which means the Lambert's W function has no solution. We can simply hard-code the case of 1 and 2.
Solution
104743
Largest product in a series
The four adjacent digits in the \( 1000 \)-digit number that have the greatest product are \( 9×9×8×9=5832 \).
\[ 73167176531330624919225119674426574742355349194934\\ 96983520312774506326239578318016984801869478851843\\ 85861560789112949495459501737958331952853208805511\\ 12540698747158523863050715693290963295227443043557\\ 66896648950445244523161731856403098711121722383113\\ 62229893423380308135336276614282806444486645238749\\ 30358907296290491560440772390713810515859307960866\\ 70172427121883998797908792274921901699720888093776\\ 65727333001053367881220235421809751254540594752243\\ 52584907711670556013604839586446706324415722155397\\ 53697817977846174064955149290862569321978468622482\\ 83972241375657056057490261407972968652414535100474\\ 82166370484403199890008895243450658541227588666881\\ 16427171479924442928230863465674813919123162824586\\ 17866458359124566529476545682848912883142607690042\\ 24219022671055626321111109370544217506941658960408\\ 07198403850962455444362981230987879927244284909188\\ 84580156166097919133875499200524063689912560717606\\ 05886116467109405077541002256983155200055935729725\\ 71636269561882670428252483600823257530420752963450 \]
Find the thirteen adjacent digits in the \( 1000 \)-digit number that have the greatest product. What is the value of this product?
Brute force
We are searching for the largest product of 13 adjacent digits in a 1000-digit number. We want to calculate the product of each 13 adjacent digits and find the largest one.
The 1000-digit number will be stored in a file, so the first step is to get this number as a string and remove each trailing newline (\n):
From read_file.py:
def read_file(filename):
with open(filename, "r") as file:
return file.read().replace("\n", "")
Given this string, we need to calculate the product of 13 adjacent digits, which can be done easily using math.prod(). Then, simply repeat this step for all 13 adjacent digits contained in the 1000-digit number and save the maximum of these products.
From solution1.py:
def largest_product_in_series(n, adj=13):
res = 0
for i in range(len(n) - adj):
res = max(prod(int(digit) for digit in n[i : i + adj]), res)
return res
0 are useless
The problem requires calculating a product, a product of something and 0 will always give a result of 0. Which means that every 13 adjacent digits containing 0 are useless since the result will never be the largest product.
The 1000-digit number can actually be split around each 0, of course if a number has less than 13 digits it can be deleted.
From solution2.py:
def split_series(n):
return [sub_n for sub_n in n.split("0") if len(sub_n) >= 13]
Another improvement reside in not calculating every product from the start, for example if we search the product of 3 adjacent digits in 12345, the 3 solutions are:
1*2*3 = 6
2*3*4 = (6 / 1) * 4 = 24
3*4*5 = (24 / 3) * 5 = 60
The second product is the same as the first, just divide the digit that is not present and multiply the one that is. We have to be careful with the digit 0 because division by 0 is an error, but we have already solved the problem just before, so we can assume our number will never contain the digit 0.
From solution2.py:
def largest_product_in_series(n, adj=13):
res = 0
current = prod(int(digit) for digit in n[0:adj])
for i in range(len(n) - adj):
current = (current // int(n[i])) * int(n[i + adj])
res = max(res, current)
return res
We simply repeat this step for each sub-number of the 1000-digit split around 0.
From solution2.py:
def largest_product_in_multiples_series(sub_n, adj=13):
res = 0
for n in sub_n:
res = max(largest_product_in_series(n, adj), res)
return res
Solution
23514624000
Special Pythagorean triplet
A Pythagorean triplet is a set of three natural numbers, \( a<b<c \), for which,
\[ a^{2} + b^{2} = c^{2} \]
For example, \( 3^{2}+4^{2}=9+16=25=5^{2} \).
There exists exactly one Pythagorean triplet for which \( a+b+c=1000 \). Find the product \( abc \).
Brute force
We are searching for \( a \), \( b \) and \( c \) such that \( a < b < c \), \( a + b + c = 1000 \) and \( a^2 + b^2 = c^2 \). The brute force solution will simply iterate to 1000 for \( a \), \( b \) and \( c \) and stop when the above equations are true.
From solution1.py:
def special_pythagorean_triplet():
for a in range(1001):
for b in range(a + 1, 1001):
for c in range(b + 1, 1001):
if a + b + c == 1000 and a**2 + b**2 == c**2:
return a * b * c
return -1
With a little thought
The Brute force solution can be simplified a bit knowing that \( a + b + c = 1000 \) implies \( c = 1000 - a - b \). This removes a for loop and an equation, since \( a + b + c = 1000 \) will always be true.
Another simplification can be made by knowing that \( a < b < c \). This implies that \( a \), \( b \) and \( c \) are lower than 500, otherwise \( a + b + c \) will be greater than 1000.
This gives us the following :
From solution2.py:
def special_pythagorean_triplet():
for a in range(501):
for b in range(a + 1, 501):
c = 1000 - a - b
if a**2 + b**2 == c**2:
return a * b * c
return -1
Prime Pythagorean triples
Given an arbitrary pair of integers m and n with m > n > 0. Euclid's formula states that the integers :
\[ a = m^2 - n^2,\ b=2mn,\ c=m^2+n^2 \]
form a Pythagorean triple: \( a^2 + b^2 = c^2 \)
If we calculate \( a^2 + b ^2 \):
\[ a^2 + b^2 = (m^2-n^2)^2 + (2mn)^2 = m^2 + 4m^2n^2 - 2m^2n^2 + n^2 = (m^2 + n^2)^2 = c^2 \]
Which is coherent, the problem changes from finding \( a \), \( b \) and \( c \) to finding \( m \) and \( n \), we have:
\[ \begin{align} a+b+c &= 1000\\ 2mn + 2m^2 &= 1000\\ n &= \frac{500}{m} - m\\ \end{align} \]
We have \( m > n \) since b must be positive, solving \( n = m \) gives:
\[ \begin{align} m &= \frac{500}{m} - m\\ 0 &= \frac{500 - 2m^2}{m}\\ 0 &= 500 - 2m^2\\ m &= \sqrt(250)\\ \end{align} \]
Resulting in:
\[ m > 16 > \sqrt(250) \]
We also have \( n > 0 \), solving \( n = 0 \) gives:
\[ \begin{align} 0 &= \frac{500}{m} - m\\ 0 &= 500 - m^2\\ m &= \sqrt(500)\\ \end{align} \]
Resulting in:
\[ m < \sqrt(500) < 23 \]
We also know that \( \frac{500}{m} \) is an integer, so m must divide \( 500 \). The only multiple of that divides \( 500 \) with the constraint \( 16 > m > 23 \) is 20. Having \( m = 20 \) result in \( n = 5 \). It gives \( a = 200 \), \( b = 375 \) and \( c \) = 425.
The solution can also be found by using a for loop to find \( m \) and \( n \) with the above constraints.
From solution3.py:
def special_pythagorean_triplet():
for m in range(16, 24):
for n in range(1, m):
if m * (n + m) == 500:
return 2 * m * n * (m**4 - n**4)
return -1
Solution
31875000
Summation of primes
The sum of the primes below \( 10 \) is \( 2+3+5+7=17 \).
Find the sum of all the primes below two million.
Brute force
We already know, thanks to te previous problems that when one search for all prime numbers below a certain limit, the sieve of eratosthenes is a good solution.
It is enough to sum the list of the primes found with the sieve.
From solution1.py:
def summation_of_primes(limit=2000000):
return sum(sieve.primerange(limit))
Summation minus summation
The sieve of eratosthenes is actually quite slow, it's possible to find a better solution if we consider that we don't need to know all the primes to find their sum. For example, the sum of the primes less than \( 10 \) is \( 2 + 3 + 5 + 7 = 17 \).
The sum of the primes less than \( 10 \) is the sum of the numbers less than 10 minus the sum of the multiples of the primes less than \( \sqrt{10} \) plus the primes themselves minus \( 1 \). In this example, the sum of the multiples of \( 2 \) and \( 3 \):
\[ \begin{alignat}{1} P &&= &&+1&&+2&&+3&&+4&&+5&&+6+7&&+8&&+9&&+10\\ &&&&&&-2&&&&-4&&&&-6&&-8&&&&-10\\ &&&&&&&&-3&&&&&&-6&&&&-9\\ &&&&-1&&+2&&+3\\ P &&= &&&&+2&&+3&&&&+5&&-6+7\\ \end{alignat} \]
There is just one problem, the number \( 6 \) is both a multiple of \( 2 \) and \( 3 \). This means we have to remove the multiple of \( 3 \) but not the multiple of \( 6 \). For numbers larger than 10, if we continue with \( 5 \) we have to remove the multiple of \( 5 \) but not the multiple of \( 2*5=10 \), \( 3*5=15 \) and \( 5*6=30 \).
Let \( \phi(n) \) be the sum of the numbers less than \( n \).
We have the following sequence:
\[ \begin{align} T_0(n) &= \phi(\left\lfloor n \right\rfloor) &&= 1+2+3+\dots\\ T_1(n) &= 2\left(T_0\left(\frac{n}{2}\right)\right) = 2\phi\left (\left\lfloor \frac{n} {2} \right\rfloor \right) &&= 2+4+6+\dots\\ T_2(n) &= 3\left(T_0\left(\frac{n}{3}\right) - T_1\left(\frac{n}{3}\right) \right) = 3\phi \left(\left\lfloor \frac{n}{3} \right\rfloor\right) - 6\phi\left(\left\lfloor \frac{n}{6} \right\rfloor\right) &&= 3+9+15+\dots\\ T_3(n) &= 5\left(T_0\left(\frac{n}{5}\right) - T_1\left(\frac{n}{5}\right) - T_2\left(\frac{n}{5}\right) \right) = 5\phi\left(\left\lfloor\frac{n}{5}\right\rfloor\right) - 10\phi\left(\left\lfloor\frac{n}{10}\right\rfloor\right) - 15\phi\left(\left\lfloor\frac{n}{15} \right\rfloor\right) + 30\phi\left(\left\lfloor\frac{n}{30} \right\rfloor\right) &&= 5+25+35+\dots\\ \end{align} \]
So the k-th term is:
\[ T_k(n) = p_k\left(T_0\left(\frac{n}{p_k}\right) - \dots - T_{k-1}\left (\frac{n} {p_k}\right)\right) \]
Where \( p_k \) is the k-th prime.
We can create a function to find \( T_k \) if we have \( p_k \):
From solution2.py:
def tk(n, k, primes):
pk = primes[k - 1]
t0 = phi(floor(n / pk))
tn = sum(tk(n / pk, i, primes) for i in range(1, k))
return pk * (t0 - tn)
The sum of the primes less than \( n \) is the sum of the numbers less than \( n \) minus the sum of all the multiples of the primes less than \( \sqrt {n} \) plus the primes themselves minus \( 1 \):
\[ \left(T_0(n) - T_1(n) - \dots - T_k(n)\right) + \left(p_1 + p_2 + \dots + p_k\right) - 1 \]
From solution2.py:
def summation_of_primes(limit=2000):
primes = list(sieve.primerange(floor(sqrt(limit)) + 1))
return phi(limit) - sum(tk(limit, i + 1, primes) for i in range(len(primes))) + sum(primes) - 1
Dynamic programming
The Summation minus summation solution gives an interesting solution because we found the sum of the primes less than \( n \) with only the primes less than \( \sqrt{n} \). Unfortunately, this solution is not efficient because it requires too much recursion for larger n.
The main problem with the previous solution was to remove the numbers that were multiples of previous primes. For example with the multiples of \( 3 \), the number \( 6 \) was already removed by the multiples of \( 2 \).
What we really want is to remove the multiples of \( 3 \) that have not already been removed by the multiples of \( 2 \) such as \( 6 \), \( 12 \) ... For \( 5 \) that would be the number that are neither multiples of \( 2 \) nor \( 3 \).
Instead of the sum of the multiples of a prime, we will search for the sum of integer that remain after sieving with all primes smaller than the current one.
This solution is well explained by Lucy_Hedgehog in this thread (only available if you solve the problem):
The main idea is as follows: Let \( S(v,m) \) be the sum of integers in the range \( 2 \dots v \) that remain after sieving with all primes smaller or equal than \( m \). That is \( S(v,m) \) is the sum of integers up to \( v \) that are either prime or the product of primes larger than \( m \).
\( S(v, p) \) is equal to \(S(v, p-1) \) if \( p \) is not prime or \( v \) is smaller than \( p*p \). Otherwise (\( p \) prime, \( p*p\leqslant v \)) \( S(v,p) \) can be computed from \(S(v, p-1)\) by finding the sum of integers that are removed while sieving with \( p \). An integer is removed in this step if it is the product of \(p \) with another integer that has no divisor smaller than \(p \). This can be expressed as
\[ S\left(v, p \right) = S\left(v, p - 1\right) - p\left(S\left(\frac{v}{p}, p - 1\right) -S\left(p-1, p-1\right)\right) \]
Dynamic programming can be used to implement this. It is sufficient to compute \( S(v,p) \) for all positive integers \( v \) that are representable as \( \left\lfloor\frac{n}{k}\right\rfloor \) for some integer \( k \) and all.
From solution3.py:
def partial_prime_sum(n=2000000):
r = ceil(sqrt(n))
V = [n // i for i in range(1, r + 1)]
V += list(range(V[-1] - 1, 0, -1))
S = {i: i * (i + 1) // 2 - 1 for i in V}
for p in range(2, r + 1):
if S[p] > S[p - 1]: # p is prime
sp = S[p - 1] # sum of primes smaller than p
p2 = p * p
for v in V:
if v < p2:
break
S[v] -= p * (S[v // p] - sp)
return S[n]
Solution
142913828922
Largest product in a grid
In the \( 20×20 \) grid below, four numbers along a diagonal line have been marked in red.
\[ 08\ 02\ 22\ 97\ 38\ 15\ 00\ 40\ 00\ 75\ 04\ 05\ 07\ 78\ 52\ 12\ 50\ 77\ 91\ 08\\ 49\ 49\ 99\ 40\ 17\ 81\ 18\ 57\ 60\ 87\ 17\ 40\ 98\ 43\ 69\ 48\ 04\ 56\ 62\ 00\\ 81\ 49\ 31\ 73\ 55\ 79\ 14\ 29\ 93\ 71\ 40\ 67\ 53\ 88\ 30\ 03\ 49\ 13\ 36\ 65\\ 52\ 70\ 95\ 23\ 04\ 60\ 11\ 42\ 69\ 24\ 68\ 56\ 01\ 32\ 56\ 71\ 37\ 02\ 36\ 91\\ 22\ 31\ 16\ 71\ 51\ 67\ 63\ 89\ 41\ 92\ 36\ 54\ 22\ 40\ 40\ 28\ 66\ 33\ 13\ 80\\ 24\ 47\ 32\ 60\ 99\ 03\ 45\ 02\ 44\ 75\ 33\ 53\ 78\ 36\ 84\ 20\ 35\ 17\ 12\ 50\\ 32\ 98\ 81\ 28\ 64\ 23\ 67\ 10\ \color{red}{26}\ 38\ 40\ 67\ 59\ 54\ 70\ 66\ 18\ 38\ 64\ 70\\ 67\ 26\ 20\ 68\ 02\ 62\ 12\ 20\ 95\ \color{red}{63}\ 94\ 39\ 63\ 08\ 40\ 91\ 66\ 49\ 94\ 21\\ 24\ 55\ 58\ 05\ 66\ 73\ 99\ 26\ 97\ 17\ \color{red}{78}\ 78\ 96\ 83\ 14\ 88\ 34\ 89\ 63\ 72\\ 21\ 36\ 23\ 09\ 75\ 00\ 76\ 44\ 20\ 45\ 35\ \color{red}{14}\ 00\ 61\ 33\ 97\ 34\ 31\ 33\ 95\\ 78\ 17\ 53\ 28\ 22\ 75\ 31\ 67\ 15\ 94\ 03\ 80\ 04\ 62\ 16\ 14\ 09\ 53\ 56\ 92\\ 16\ 39\ 05\ 42\ 96\ 35\ 31\ 47\ 55\ 58\ 88\ 24\ 00\ 17\ 54\ 24\ 36\ 29\ 85\ 57\\ 86\ 56\ 00\ 48\ 35\ 71\ 89\ 07\ 05\ 44\ 44\ 37\ 44\ 60\ 21\ 58\ 51\ 54\ 17\ 58\\ 19\ 80\ 81\ 68\ 05\ 94\ 47\ 69\ 28\ 73\ 92\ 13\ 86\ 52\ 17\ 77\ 04\ 89\ 55\ 40\\ 04\ 52\ 08\ 83\ 97\ 35\ 99\ 16\ 07\ 97\ 57\ 32\ 16\ 26\ 26\ 79\ 33\ 27\ 98\ 66\\ 88\ 36\ 68\ 87\ 57\ 62\ 20\ 72\ 03\ 46\ 33\ 67\ 46\ 55\ 12\ 32\ 63\ 93\ 53\ 69\\ 04\ 42\ 16\ 73\ 38\ 25\ 39\ 11\ 24\ 94\ 72\ 18\ 08\ 46\ 29\ 32\ 40\ 62\ 76\ 36\\ 20\ 69\ 36\ 41\ 72\ 30\ 23\ 88\ 34\ 62\ 99\ 69\ 82\ 67\ 59\ 85\ 74\ 04\ 36\ 16\\ 20\ 73\ 35\ 29\ 78\ 31\ 90\ 01\ 74\ 31\ 49\ 71\ 48\ 86\ 81\ 16\ 23\ 57\ 05\ 54\\ 01\ 70\ 54\ 71\ 83\ 51\ 54\ 69\ 16\ 92\ 33\ 48\ 61\ 43\ 52\ 01\ 89\ 19\ 67\ 48 \]
The product of these numbers is \( 26×63×78×14=1788696 \).
What is the greatest product of four adjacent numbers in the same direction (up, down, left, right, or diagonally) in the \( 20×20 \) grid?
Brute force
This problem is not interesting, the solution is simply to iterate on each row, column and on the two diagonal.
As with Largest product in a series, the input grid will be stored in a file, so the first step is to obtain this grid as int matrix.
From read_file.py:
def read_file(filename):
with open(filename, "r") as file:
return [
[int(x) for x in line.split(" ")] for line in file.read().split("\n")[:-1]
]
And then just iterate on this matrix:
From solution1.py:
def largest_product_in_grid(filename):
g = read_file(filename)
for y in range(0, 20):
for x in range(0, 17):
yield g[x][y] * g[x + 1][y] * g[x + 2][y] * g[x + 3][y]
for x in range(0, 20):
for y in range(0, 17):
yield g[x][y] * g[x][y + 1] * g[x][y + 2] * g[x][y + 3]
for y in range(0, 17):
for x in range(0, 17):
yield g[x][y] * g[x + 1][y + 1] * g[x + 2][y + 2] * g[x + 3][y + 3]
for x in range(3, 20):
for y in range(0, 17):
yield g[x][y] * g[x - 1][y + 1] * g[x - 2][y + 2] * g[x - 3][y + 3]
Solution
70600674
Highly divisible triangular number
The sequence of triangle numbers is generated by adding the natural numbers. So the \( 7^{th} \) triangle number would be \( 1+2+3+4+5+6+7=28 \). The first ten terms would be:
\[ 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ... \]
Let us list the factors of the first seven triangle numbers:
\[ \begin{align} 1&: 1\\ 3&: 1,3\\ 6&: 1,2,3,6\\ 10&: 1,2,5,10\\ 15&: 1,3,5,15\\ 21&: 1,3,7,21\\ 28&: 1,2,4,7,14,28\end{align} \]
We can see that \( 28 \) is the first triangle number to have over five divisors.
What is the value of the first triangle number to have over five hundred divisors?
Brute force
Finding the number of factors of \( n \) can be done by iterating from 1 to \( n \) and checking each number that can divide \( n \).
From solution1.py:
def number_of_factors(n):
res = 1
for i in range(2, n):
if n % i == 0:
res += 1
return res
Triangular number can be computed quite easily with a loop, we can generate them as long as their number of divisor is less than \( 500 \).
From solution1.py:
def highly_div_triangular_number(n=500):
i = 1
res = 1
while number_of_factors(res) < n:
i += 1
res += i
return res
Common factor
The Brute Force solution is really slow, way to slow to be honest.
First, we can improve the way we find the number of factors. If \( i \) divides \( n \), then obviously \( \frac{n}{i} \) divides \( n \) too. We do not need to iterate from 2 to \( n \) but only to \( \sqrt{n} \) and add the factors two by two. The only exception is that if \( \sqrt{n} \) divides \( n \) we only need to count it once.
From solution2.py:
def number_of_factors(n):
res = 1
root = floor(sqrt(n))
for i in range(2, root):
if n % i == 0:
res += 1
return 2 * res + (root**2 == n)
This makes the solution much faster, but there is still room for improvement in the way the triangular numbers are calculated. We already know from the previous problems that the sum of integer from \( 1 \) to \( n \) is \(\frac{n(n+1) }{2} \). Since \( n \) and \( n + 1 \) have no factors in common except \( 1 \), we can multiply the number of factor in \( \frac{n}{2} \) and \( n + 1 \) or \( n \) and \( \frac{n+1}{2} \) depending on the parity of \( n \). This allows us to calculate the number of factors of smaller numbers, which makes the solution quite fast compared to the Brute force solution.
From solution2.py:
def highly_div_triangular_number(n=500):
i = 0
factors = 0
while factors < n:
i += 1
if i % 2 == 0:
factors = number_of_factors(i // 2) * number_of_factors(i + 1)
else:
factors = number_of_factors(i) * number_of_factors((i + 1) // 2)
return i * (i + 1) // 2
Solution
76576500
Large sum
Work out the first ten digits of the sum of the following one-hundred \( 50 \)-digit numbers.
\[ 37107287533902102798797998220837590246510135740250\\\\ 46376937677490009712648124896970078050417018260538\\\\ 74324986199524741059474233309513058123726617309629\\\\ 91942213363574161572522430563301811072406154908250\\\\ 23067588207539346171171980310421047513778063246676\\\\ 89261670696623633820136378418383684178734361726757\\\\ 28112879812849979408065481931592621691275889832738\\\\ 44274228917432520321923589422876796487670272189318\\\\ 47451445736001306439091167216856844588711603153276\\\\ 70386486105843025439939619828917593665686757934951\\\\ 62176457141856560629502157223196586755079324193331\\\\ 64906352462741904929101432445813822663347944758178\\\\ 92575867718337217661963751590579239728245598838407\\\\ 58203565325359399008402633568948830189458628227828\\\\ 80181199384826282014278194139940567587151170094390\\\\ 35398664372827112653829987240784473053190104293586\\\\ 86515506006295864861532075273371959191420517255829\\\\ 71693888707715466499115593487603532921714970056938\\\\ 54370070576826684624621495650076471787294438377604\\\\ 53282654108756828443191190634694037855217779295145\\\\ 36123272525000296071075082563815656710885258350721\\\\ 45876576172410976447339110607218265236877223636045\\\\ 17423706905851860660448207621209813287860733969412\\\\ 81142660418086830619328460811191061556940512689692\\\\ 51934325451728388641918047049293215058642563049483\\\\ 62467221648435076201727918039944693004732956340691\\\\ 15732444386908125794514089057706229429197107928209\\\\ 55037687525678773091862540744969844508330393682126\\\\ 18336384825330154686196124348767681297534375946515\\\\ 80386287592878490201521685554828717201219257766954\\\\ 78182833757993103614740356856449095527097864797581\\\\ 16726320100436897842553539920931837441497806860984\\\\ 48403098129077791799088218795327364475675590848030\\\\ 87086987551392711854517078544161852424320693150332\\\\ 59959406895756536782107074926966537676326235447210\\\\ 69793950679652694742597709739166693763042633987085\\\\ 41052684708299085211399427365734116182760315001271\\\\ 65378607361501080857009149939512557028198746004375\\\\ 35829035317434717326932123578154982629742552737307\\\\ 94953759765105305946966067683156574377167401875275\\\\ 88902802571733229619176668713819931811048770190271\\\\ 25267680276078003013678680992525463401061632866526\\\\ 36270218540497705585629946580636237993140746255962\\\\ 24074486908231174977792365466257246923322810917141\\\\ 91430288197103288597806669760892938638285025333403\\\\ 34413065578016127815921815005561868836468420090470\\\\ 23053081172816430487623791969842487255036638784583\\\\ 11487696932154902810424020138335124462181441773470\\\\ 63783299490636259666498587618221225225512486764533\\\\ 67720186971698544312419572409913959008952310058822\\\\ 95548255300263520781532296796249481641953868218774\\\\ 76085327132285723110424803456124867697064507995236\\\\ 37774242535411291684276865538926205024910326572967\\\\ 23701913275725675285653248258265463092207058596522\\\\ 29798860272258331913126375147341994889534765745501\\\\ 18495701454879288984856827726077713721403798879715\\\\ 38298203783031473527721580348144513491373226651381\\\\ 34829543829199918180278916522431027392251122869539\\\\ 40957953066405232632538044100059654939159879593635\\\\ 29746152185502371307642255121183693803580388584903\\\\ 41698116222072977186158236678424689157993532961922\\\\ 62467957194401269043877107275048102390895523597457\\\\ 23189706772547915061505504953922979530901129967519\\\\ 86188088225875314529584099251203829009407770775672\\\\ 11306739708304724483816533873502340845647058077308\\\\ 82959174767140363198008187129011875491310547126581\\\\ 97623331044818386269515456334926366572897563400500\\\\ 42846280183517070527831839425882145521227251250327\\\\ 55121603546981200581762165212827652751691296897789\\\\ 32238195734329339946437501907836945765883352399886\\\\ 75506164965184775180738168837861091527357929701337\\\\ 62177842752192623401942399639168044983993173312731\\\\ 32924185707147349566916674687634660915035914677504\\\\ 99518671430235219628894890102423325116913619626622\\\\ 73267460800591547471830798392868535206946944540724\\\\ 76841822524674417161514036427982273348055556214818\\\\ 97142617910342598647204516893989422179826088076852\\\\ 87783646182799346313767754307809363333018982642090\\\\ 10848802521674670883215120185883543223812876952786\\\\ 71329612474782464538636993009049310363619763878039\\\\ 62184073572399794223406235393808339651327408011116\\\\ 66627891981488087797941876876144230030984490851411\\\\ 60661826293682836764744779239180335110989069790714\\\\ 85786944089552990653640447425576083659976645795096\\\\ 66024396409905389607120198219976047599490197230297\\\\ 64913982680032973156037120041377903785566085089252\\\\ 16730939319872750275468906903707539413042652315011\\\\ 94809377245048795150954100921645863754710598436791\\\\ 78639167021187492431995700641917969777599028300699\\\\ 15368713711936614952811305876380278410754449733078\\\\ 40789923115535562561142322423255033685442488917353\\\\ 44889911501440648020369068063960672322193204149535\\\\ 41503128880339536053299340368006977710650566631954\\\\ 81234880673210146739058568557934581403627822703280\\\\ 82616570773948327592232845941706525094512325230608\\\\ 22918802058777319719839450180888072429661980811197\\\\ 77158542502016545090413245809786882778948721859617\\\\ 72107838435069186155435662884062257473692284509516\\\\ 20849603980134001723930671666823555245252804609722\\\\ 53503534226472524250874054075591789781264330331690 \]
Brute force
The main problem is to find a way to add large numbers, because computers can not store large numbers so easily. That's the point of the problem, to find a way to add those numbers. We could use an array to store each digit of each number and add them, but thanks to python and the unifying long integers and integers we can just add these numbers without worrying about memory.
We just need to get the first 10 digits of the additions, which can be done quite easily by converting the number to a string ang get the first 10 characters.
From solution1.py:
def large_sum(filename):
return str(sum(read_file(filename)))[:10]
Solution
5537376230
Longest Collatz sequence
The following iterative sequence is defined for the set of positive integers:
\[ \begin{align} & n \rightarrow \frac{n}{2}\ (n\ is\ even)\\ & n \rightarrow 3n + 1\ (n\ is\ odd) \end{align} \]
Using the rule above and starting with \( 13 \), we generate the following sequence:
\[ 13 \rightarrow 40 \rightarrow 20 \rightarrow 10 \rightarrow 5 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1 \]
It can be seen that this sequence (starting at \( 13 \) and finishing at \( 1 \)) contains \( 10 \) terms. Although it has not been proved yet (Collatz Problem), it is thought that all starting numbers finish at \( 1 \).
Which starting number, under one million, produces the longest chain?
NOTE: Once the chain starts the terms are allowed to go above one million.
Brute force
Calculating the number of iterations of the Collatz sequence is easy, just follow the sequence until it reaches one, and count the number of iterations to get there:
From solution1.py:
def collatz(n):
iteration = 0
while n != 1:
n = n // 2 if n % 2 == 0 else 3 * n + 1
iteration += 1
return iteration
Then, just check the iteration for each starting number from 1 to 1000000 and return the largest.
From solution1.py:
def longest_collatz_sequence(n=1000000):
res, max_it = 0, 0
for i in range(1, n):
current_it = collatz(i)
if current_it > max_it:
res, max_it = i, current_it
return res
Caching
The Collatz sequence of starting numbers \( 4 \) and \( 8 \) are actually quite similar : \[ \begin{align} &Collatz(4) = 4 \rightarrow 2 \rightarrow 1\\ &Collatz(8) = 8 \rightarrow 4 \rightarrow 2 \rightarrow 1\\ \end{align} \]
By calculating \( Collatz(8) \) we ended up recalculating \( Collatz(4) \), if we keep in memory the number of iterations of \( Collatz(4) \), we could reuse it to find the number of iterations of \( Collatz(8) \).
That is what cache is, storing data so that future requests for that data can be served faster.
In our case, when calculating the number of iteration of \( n \), we first look if the value has already been computed, if not, we update the cache using the formula.
From solution2.py:
def longest_collatz_sequence(n=1000000):
cache = {1: 1}
def collatz(i):
if i not in cache:
cache[i] = collatz(i // 2 if i % 2 == 0 else 3 * i + 1) + 1
return cache[i]
return max(range(1, n), key=collatz)
Solution
837799
Lattice paths
Starting in the top left corner of a \( 2×2 \) grid, and only being able to move to the right and down, there are exactly \( 6 \) routes to the bottom right corner.
How many such routes are there through a \( 20×20 \) grid?
Brute force
We are searching for the number of different paths starting from the top left corner and going to the bottom right corner of a \( 20 \times 20 \) square. The only possible moves are down and right. This is the same as searching for the Lattice path.
Since the square is \( 20 \times 20 \) we have 20 moves down and 20 moves to the right. If we move to the right, then we have 20 moves down and 19 moves to the right, we can continue as long as we have moves available.
The solution can be done recursively, starting with 20 moves down and right, the result being the combination of paths down and to the right. Each times we move down we call the function recursively with the same number of moves to the right, but one less move down. When the number of move down is 1, the result is obviously 1: the only remaining path is the one to the right. The same can be done for the move to the right.
From solution1.py:
def lattice_paths(up=20, down=20):
moves_down = lattice_paths(up, down - 1) if down > 1 else 1
moves_up = lattice_paths(up - 1, down) if up > 1 else 1
return moves_up + moves_down
Dynamic programming
The Brute force solution is not efficient at all, for example, if we go down and then right or right and then down, we end up in the same place. The Brute force solution will compute the answer twice.
We could use a cache, but let's do this solution iteratively rather than recursively.
We can represent the solution using a matrix, for example, for a \( 3 \times 3 \) square, we have the number of paths from the green point to the red point for each sub parallelogram.
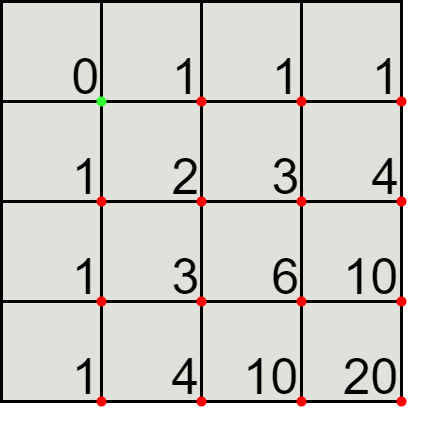
Looking at the \( 2 \times 2 \) sub square, we can see that the number of different paths is indeed 6.
For each red point, the number of different paths to it is the sum of the path above and paths on the left.
For the first row and column, the number of different paths is one: either only downs or only rights. Then, we can simply compute the path to the other red points using the old ones, we simply return the value at the last cell.
From solution2.py:
def lattice_paths(n=20):
n += 1
paths = np.zeros((n, n), dtype=int)
for i in range(1, n):
paths[i, 0] = 1
paths[0, i] = 1
for i in range(1, n):
for j in range(1, n):
paths[i, j] = paths[i - 1, j] + paths[i, j - 1]
return paths[n - 1, n - 1]
Combination
For a square of dimension \( n \), we know that whatever path we take, there will be exactly \( n \) movements to the right and \( n \) movements down. We can represent the path as a string of 'D' for down and 'R' for right.
For example, with a \( 3 \times 3 \) square, a path could be : 'RRRDDD', 'DDDRRR' or 'RDDRDR'. The question now is, 'In how many ways can we place the ' R' and the 'D' in the string ?'
Since there must be as many 'D' as 'R', we can only place the 'R' and leave the rest as 'D'. That means we are searching for the number of ways we can place \( n \) 'R' in a string of \( 2n \) characters. This is called a combination, in our case, it's:
\[ \begin{pmatrix} 2n\\ n \end{pmatrix} = \frac{\left(2n\right)!}{n!\left(2n - n\right)!} = \frac{\left (2n\right)!}{\left(n!\right)^2} \]
This can be calculated using factorial:
From solution3.py:
def lattice_paths(n=20):
return factorial(2 * n) // (factorial(n) ** 2)
Solution
137846528820
Power digit sum
\( 2^{15}=32768 \) and the sum of its digits is \( 3+2+7+6+8=26 \).
What is the sum of the digits of the number \( 2^{1000} \)?
Brute force
Thanks to python, the solution is trivial, we just need to sum the digits of a number, which can be done by casting it into a string and iterating on it.
From solution1.py:
def power_digit_sum(n=1000):
return sum((int(d) for d in str(2**n)))
Solution
1366
Number letter counts
If the numbers \( 1 \) to \( 5 \) are written out in words: one, two, three, four, five, then there are \( 3+3+5+4+4=19 \) letters used in total.
If all the numbers from \( 1 \) to \( 1000 \) (one thousand) inclusive were written out in words, how many letters would be used?
NOTE: Do not count spaces or hyphens. For example, \( 342 \) (three hundred and forty-two) contains \( 23 \) letters and \( 115 \) (one hundred and fifteen) contains \( 20 \) letters. The use of "and" when writing out numbers is in compliance with British usage.
Brute force
This problem is boring, there is nothing interesting to do, we can only count some word several times. For example, the word "hundred" is used 900 times from 100 to 999, this allows some factoring. We can do the same for the number from 1 to 9, for "and", for 10, 20, 30, ...
From solution1.py:
def number_letter_counts():
unit = len("onetwothreefourfivesixseveneightnine")
ten = len("teneleventwelvethirfourfifsixseveneighnine") + len("ten") * 7
and_l = len("and")
twenty = len("twentythirtyfortyfiftysixtyseventyeightyninety")
hun = len("hundred")
thou = len("onethousand")
return thou + 900 * hun + 190 * unit + 100 * twenty + 891 * and_l + 10 * ten
Solution
21124
Maximum path sum I
By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is \( 23 \).
\[ \color{red}{3}\\\\ 2\ \color{red}{4}\ 6\\\\ 8\ 5\ \color{red}{9}\ 3 \]
That is, \( 3+7+4+9=23 \).
Find the maximum total from top to bottom of the triangle below:
\[ 75\\\\ 95\ 64\\\\ 17\ 47\ 82\\\\ 18\ 35\ 87\ 10\\\\ 20\ 04\ 82\ 47\ 65\\\\ 19\ 01\ 23\ 75\ 03\ 34\\\\ 88\ 02\ 77\ 73\ 07\ 63\ 67\\\\ 99\ 65\ 04\ 28\ 06\ 16\ 70\ 92\\\\ 41\ 41\ 26\ 56\ 83\ 40\ 80\ 70\ 33\\\\ 41\ 48\ 72\ 33\ 47\ 32\ 37\ 16\ 94\ 29\\\\ 53\ 71\ 44\ 65\ 25\ 43\ 91\ 52\ 97\ 51\ 14\\\\ 70\ 11\ 33\ 28\ 77\ 73\ 17\ 78\ 39\ 68\ 17\ 57\\\\ 91\ 71\ 52\ 38\ 17\ 14\ 91\ 43\ 58\ 50\ 27\ 29\ 48\\\\ 63\ 66\ 04\ 68\ 89\ 53\ 67\ 30\ 73\ 16\ 69\ 87\ 40\ 31\\\\ 04\ 62\ 98\ 27\ 23\ 09\ 70\ 98\ 73\ 93\ 38\ 53\ 60\ 04\ 23 \]
NOTE: As there are only \( 16384 \) routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o)
Brute force
Even if the problem tells us not to use brute force, we will still do it. Not because we want to do things easily, but because it will be much easier to find a better solution later after solving the problem the first time.
First, we need to transform the triangle into something easier to manipulate, for example a two-dimensional array.
The problem can be solved quite easily after that, with a simple recursion: The maximum score is the current number plus the highest score by choosing the left or the right.
It is enough to stop when we are outside the triangle, since the lower number is 0, we can consider that leaving the triangle is like adding 0.
From solution1.py:
def maximum_path_sum_I(filename):
triangle = read_file(filename)
def path(i, j):
if i >= len(triangle) or j >= len(triangle[i]):
return 0
return triangle[i][j] + max(path(i + 1, j), path(i + 1, j + 1))
return path(0, 0)
Dynamic programming
The Brute force solution has some issue, for example with the following triangle:
\[ \begin{gather} 01\\ 02\quad 03\\ 04\quad \color{red}{05}\quad 06\\ 07\quad \color{green}{08}\quad \color{green}{09}\quad 10\\ \end{gather} \]
The path \( 1 \rightarrow 2 \rightarrow 5 \) and the path \( 1 \rightarrow 3 \rightarrow 5 \) both end on 5 and then try to find the best solution between 8 and 9. Obviously, the best choice is 9, because it is the largest number between 8 and 9 and there is no path left to take. It doesn't depend on where we come from, which means that we can replace the number 5 with \( 5 + 9 = 14 \). We can do the same with 4 and 6, which then gives the following triangle:
\[ \begin{gather} 01\\ 02\quad 03\\ \color{red}{12}\quad \color{red}{14}\quad \color{red}{16}\\ 07\quad 08\quad 09\quad 10\\ \end{gather} \]
And we can go all the way to the end by reducing the last line each time:
\[ \begin{gather} 01\\ \color{red}{16}\quad \color{red}{19}\\ 12\quad 14\quad 16\\ 07\quad 08\quad 09\quad 10\\ \end{gather} \]
And finally:
\[ \begin{gather} \color{red}{20}\\ 16\quad 19\\ 12\quad 14\quad 16\\ 07\quad 08\quad 09\quad 10\\ \end{gather} \]
This solution is much faster because it doesn't recalculate anything twice, it just chooses the best path from the end, since we don't need to know where we came from to find the best incoming path.
From solution2.py:
def maximum_path_sum_I(filename):
triangle = read_file(filename)
for i in range(len(triangle) - 2, -1, -1):
for j in range(len(triangle[i])):
triangle[i][j] += max(triangle[i + 1][j], triangle[i + 1][j + 1])
return triangle[0][0]
Solution
1074
Counting Sundays
You are given the following information, but you may prefer to do some research for yourself.
- 1 Jan 1900 was a Monday.
- Thirty days has September,
April, June and November.
All the rest have thirty-one,
Saving February alone,
Which has twenty-eight, rain or shine.
And on leap years, twenty-nine.- A leap year occurs on any year evenly divisible by 4, but not on a century unless it is divisible by 400.
How many Sundays fell on the first of the month during the twentieth century (\( 1 \) Jan \( 1901 \) to \( 31 \) Dec \( 2000 \))?
Brute force
This problem is not fascinating, we could start from the first of January 1901 as a Tuesday, and iterate on each month, for example the first day of February 1901 is Tuesday + \( 31\ \%\ 7 \), which is Friday. We could continue by taking leap year into account. But thanks to Python, we can solve this problem with a simpler solution:
From solution1.py:
def counting_sundays():
res = 0
for year in range(1901, 2001):
for month in range(1, 13):
if datetime.datetime(year, month, 1).weekday() == 6:
res += 1
return res
Solution
171
Factorial digit sum
\( n! \) means \( n × (n −1) ×...×3×2×1 \)
For example, \( 10!=10×9×...×3×2×1=3628800 \), and the sum of the digits in the number \( 10! \) is \( 3+6+2+8+8+0+0=27 \).
Find the sum of the digits in the number \( 100! \)
Brute force
As always, problems involving large numbers are easy to solve in Python, just compute the number and iterate on it as a string:
From solution1.py:
def factorial_digit_sum(n=100):
return sum(int(x) for x in str(factorial(n)))
Solution
648
Amicable numbers
Let \( d(n) \) be defined as the sum of proper divisors of \( n \) (numbers less than \( n \) which divide evenly into \( n \)).
If \( d(a) = b \) and \( d(b) = a \), where \( a ≠ b \), then \( a \) and \( b \) are an amicable pair and each of \( a \) and \( b \) are called amicable numbers.
For example, the proper divisors of \( 220 \) are \( 1 \), \( 2 \), \( 4 \), \( 5 \), \( 10 \), \( 11 \), \( 20 \), \( 22 \), \( 44 \), \( 55 \) and \( 110 \); therefore \( d(220)=284 \). The proper divisors of \( 284 \) are \( 1 \), \( 2 \), \( 4 \), \( 71 \) and \( 142 \); so \( d(284)=220 \).
Evaluate the sum of all the amicable numbers under \( 10000 \).
Brute force
The problem first requires to find the sum of proper divisors of a number, if recall, in the Problem 12: Highly divisible triangular number, we found the number of proper divisors, we can reuse this function by adding the divisors rather than counting them.
From solution1.py:
def sum_of_factors(n):
res = 1
root = floor(sqrt(n))
for i in range(2, root + 1):
if n % i == 0:
res += i + n // i
return res
We can simply iterate from 1 to 10000 and sum the amicable numbers found to find the solution, we just to be aware that even if \( d(6) = 6 \) and so \( d(6) = 6 \), 6 is not an amicable number because amicable numbers are in pairs.
From solution1.py:
def amicable_numbers(n=10000):
res = 0
for i in range(2, n):
current = sum_of_factors(i)
if i != current and i == sum_of_factors(current):
res += i
return res
Solution
31626
Names scores
Using names.txt (right click and 'Save Link/Target As...'), a 46K text file containing over five-thousand first names, begin by sorting it into alphabetical order. Then working out the alphabetical value for each name, multiply this value by its alphabetical position in the list to obtain a name score.
For example, when the list is sorted into alphabetical order, COLIN, which is worth \( 3+15+12+9+14=53 \), is the \( 938 \)th name in the list. So, COLIN would obtain a score of \( 938×53=49714 \).
What is the total of all the name scores in the file?
Brute force
We first get the huge list of names in python, we just need to remove the ""
around them.
From read_file.py:
def read_file(filename):
with open(filename, "r") as file:
return [name[1:-1] for name in file.read().split(",")]
Then we just need to sum the letters of the names by their position in the
alphabet. Since all the names are capitalized, we can remove ord('A') + 1 to
get their position in the alphabet. The last step is to sum the position of the
names in the list by its value.
From solution1.py:
def names_scores(filename):
names = read_file(filename).sort()
return sum((i + 1) * sum(ord(c) - ord("A") + 1 for c in name) for (i, name) in enumerate(names))
Solution
871198282
Non-abundant sums
A perfect number is a number for which the sum of its proper divisors is exactly equal to the number. For example, the sum of the proper divisors of \( 28 \) would be \( 1+2+4+7+14=28 \), which means that \( 28 \) is a perfect number.
A number \( n \) is called deficient if the sum of its proper divisors is less than \( n \) and it is called abundant if this sum exceeds \( n \).
As \( 12 \) is the smallest abundant number, \( 1+2+3+4+6=16 \), the smallest number that can be written as the sum of two abundant numbers is \( 24 \). By mathematical analysis, it can be shown that all integers greater than \( 28123 \) can be written as the sum of two abundant numbers. However, this upper limit cannot be reduced any further by analysis even though it is known that the greatest number that cannot be expressed as the sum of two abundant numbers is less than this limit.
Find the sum of all the positive integers which cannot be written as the sum of two abundant numbers.
Brute force
We are searching for all numbers that are not the sum of two abundant numbers. Since every integer larger than 28123 can be written as the sum of two abundant numbers, our upper limit is therefore 28123.
First, we need to find all the abundant number below 28123, going higher is pointless because we are searching for positive numbers only. An abundant number is a number that have a larger sum of divisors than itself. We already have a function to compute the sum of divisors, we just need to be aware that if \( \sqrt{n} \) divide \( n \), it only has to count once.
From solution1.py:
def sum_of_factors(n):
res = 1
root = floor(sqrt(n))
for i in range(2, root + 1):
if n % i == 0:
res += i + n // i
if root**2 == n:
res -= root
return res
We just need to check if a number is the sum of two of the abundant numbers calculated earlier. The naive way to do this is to try every combination of two abundant numbers.
From solution1.py:
def is_sum(i, abundant):
return any(a1 + a2 == i for a1 in abundant for a2 in abundant)
Finally, we just have to sum each number less than 28124 that is not the sum of two abundant numbers.
From solution1.py:
def non_abundant_sums():
abundant = [i for i in range(1, 28124) if sum_of_factors(i) > i]
return sum(i for i in range(28124) if not is_sum(i, abundant))
Set
The Brute Force solution is extremely slow, the biggest issue is how we determine if a number is the sum of two abundant numbers.
We are searching for any abundant numbers \( a_1 \) and \( a_2 \) such that \( a_1 + a_2 = n \), which implies that \(a_2 = n - a_2 \). If \( n - a_2 \) is an abundant number, then \( n \) is the sum of two abundant numbers.
Finding a value in a list is slow because we need to go through the whole list, that's why using a set to store our abundant is more efficient in our this case. We just need to iterate over all abundant once and check if \( n \) minus this abundant is also in the set.
We can also improve the way we build this set of abundant numbers. Since we have an upper bound, we can construct the sum of divisors of all these numbers at once. For every \( i \) and \( j \) such that \( i \times j < limit \), the number \( i \times j \) has both \( i \) and \( j \) as divisors. We just need to be aware that if \( i = j \) we need to add the divisor only once.
We start with a list of 1 because 1 divides all numbers. Then we iterate with \( i \) from 2 to \( \left\lfloor\sqrt{limit}\right\rfloor \) and \( j \) from \( i + 1 \) (to avoid the case where \( i = j \)) to \( i \times j > limit \Leftrightarrow j > \left\lfloor \frac{limit}{i} \right\rfloor \).
From solution2.py:
def get_sum_of_factors(n):
sum_of_factors = [1] * (n + 1)
for i in range(2, floor(sqrt(n)) + 1):
sum_of_factors[i * i] += i
for j in range(i + 1, (n // i) + 1):
sum_of_factors[i * j] += i + j
return sum_of_factors
In the previous solution, we first built the list of abundant numbers and then searched for the number that was not a sum of two of them, since we always have \( a_1 <= a_2 \) we can actually do both at the same time.
From solution2.py:
def non_abundant_sums(n=28123):
sum_of_factors = get_sum_of_factors(n)
abundant = set()
res = 0
for i in range(1, n + 1):
if sum_of_factors[i] > i:
abundant.add(i)
if all((i - a1 not in abundant) for a1 in abundant):
res += i
return res
Solution
4179871
Lexicographic permutations
A permutation is an ordered arrangement of objects. For example, \( 3124 \) is one possible permutation of the digits \( 1 \), \( 2 \), \( 3 \) and \( 4 \). If all of the permutations are listed numerically or alphabetically, we call it lexicographic order. The lexicographic permutations of \( 0 \), \( 1 \) and \( 2 \) are:
\[ 012\ \ 021\ \ 102\ \ 120\ \ 201\ \ 210 \]
What is the millionth lexicographic permutation of the digits \( 0 \), \( 1 \), \( 2 \), \( 3 \), \( 4 \), \( 5 \), \( 6 \), \( 7 \), \( 8 \) and \( 9 \)?
Brute force
First of all, we need to understand how the lexicographic permutations are computed. If we enumerate all the permutations of '0123' starting with '0':
\[ 0123\\ 0132\\ 0213\\ 0231\\ 0312\\ 0321\\ \]
By removing the '0' we get:
\[ 123\\ 132\\ 213\\ 231\\ 312\\ 321\\ \]
It's the lexicographic permutations of '123' !
We can continue:
\[\begin{align} &123\ &&213\ &&321\\ &132\ &&231\ &&321 \end{align} \]
By removing the first character each time, it gives:
\[\begin{align} &23\ &&13\ &&21\\ &32\ &&31\ &&21 \end{align} \]
That is, the lexicographic permutations of '23', '13', and '21',
Now, enumerating all permutations of '0123' starting with '1':
\[ 1023\\ 1032\\ 1203\\ 1230\\ 1302\\ 1230 \]
By removing the '1' we get:
\[ 023\\ 032\\ 203\\ 230\\ 302\\ 230 \]
It's the lexicographic permutations of '023' !
This means that we can compute all the lexicographic permutations of a string by taking each character, placing it at the beginning of the new permutations and then adding the lexicographic permutations of the rest of the string recursively.
From solution1.py:
def lexicographic_permutations(s):
if len(s) <= 1:
yield s
else:
for i in range(len(s)):
for p in lexicographic_permutations(s[:i] + s[i + 1 :]):
yield s[i] + p
By using yield, we create a generator, it's better than storing 1 million
elements and then returning the last one, just take the 1000000th element
generated.
Maths permutations
If you have understood how lexicographic permutation are constructed, you should have noticed that permutations are made from right to left. Before updating the number on the left, all permutations on the right must have been made. That is why with the string '0123', the first 6 permutations begin with '0', then the 6 following permutations with '1', and so on.
The string in our examples contains 4 characters, it implies that every \( ( 4 - 1 )! \) permutations the first digit will change. We can even tell which one will be placed first by knowing the multipliers of that factorial. If it is the \( 3 * 3! \)th permutations, the first digit will be the third one in the string, '3' in this example.
Since this process is recursive, we can find the first digit each time by reducing the n-th permutations we are looking for.
For example, if we researched the 15th lexicographic permutations, we know that the first character will be '2' because the \( 3! \) first permutations will start with '0', the next \( 3! \) with '1'.
The 12th lexicographic permutations is obviously '2013'. It's just '0123', but the '2' is place at the first position. Now that we have our first digit, we can remove those 12 permutations from the 15th, which gives us 3 permutations.
Now, we are searching for the third lexicographic permutations of '013', with the same reasoning, we can find that the first digit will be '1' after \( 1 * 2! \) permutations. It leaves use with 1 permutation and the string '03'.
After \( 1 * 1! \) permutations the first digit will be '3'. It leaves us with '0' which is the last digit. The 15 lexicographic permutations is '2130' !
We just have to find the quotient and remainder of our nth permutations, the divisor being the length of the string minus one. We can continue as long as our string contains more than one character.
From solution2.py:
def lexicographic_permutations(s, n):
if len(s) <= 1:
return s
q, r = divmod(n, factorial(len(s) - 1))
return s[q] + lexicographic_permutations(s[:q] + s[q + 1 :], r)
Solution
2783915460
1000-digit Fibonacci number
The Fibonacci sequence is defined by the recurrence relation:
\[ F_n = F_{n−1} + F_{n−2},\ where\ F_1 = 1\ and\ F_2 = 1. \]
Hence the first \( 12 \) terms will be:
\[ \begin{align} F1 &= 1\\ F2 &= 1\\ F3 &= 2\\ F4 &= 3\\ F5 &= 5\\ F6 &= 8\\ F7 &= 13\\ F8 &= 21\\ F9 &= 34\\ F10 &= 55\\ F11 &= 89\\ F12 &= 144 \end{align} \]
The \( 12 \)th term, \(F_{12} \), is the first term to contain three digits.
What is the index of the first term in the Fibonacci sequence to contain \( 1000 \) digits?
Brute force
The brute force solution is simple, just iterate until the number of digits is at least 1000. We can count the number of digits in a number by turning it into a string and counting its length.
From solution1.py:
def thousandth_digit_fibonacci_number(n=1000):
f1 = 1
f2 = 1
res = 1
while len(str(f1)) < n:
f1, f2 = f2, f1 + f2
res += 1
return res
Fibonacci convergence
We know from Fibonacci and the golden ratio that the n-th term of Fibonacci can be expressed as :
\[ F_{n} = \frac{\varphi^{n}}{\sqrt{5}} = \frac{\left(\frac{1+\sqrt{5}}{2} \right)^n}{\sqrt{5}} \]
Searching for a number with at least 1000 digit is the same as searching a for number that is greater than or equal to \( 10^{999} \)
\[ \begin{align} \frac{\varphi^{n}}{\sqrt{5}} & >= 10^{999}\\ n * \log(\varphi) - \frac{\log(5)}{2} & >= 999 * log(10)\\ n & >= \frac{\frac{\log(5)}{2} + 999}{\log(\varphi)}\\ n & = \left\lceil\frac{\frac{\log(5)}{2} + 999}{\log(\varphi)} \right\rceil\\ \end{align} \]
Since n must be an integer, it is sufficient to take the ceiling from the previous equation.
From solution2.py:
def thousandth_digit_fibonacci_number(n=1000):
return ceil((n - 1 + log10(sqrt(5)) / 2) / log10((1 + sqrt(5)) / 2))
Solution
4782
Reciprocal cycles
A unit fraction contains \( 1 \) in the numerator. The decimal representation of the unit fractions with denominators \( 2 \) to \( 10 \) are given:
\[ \begin{align} \frac{1}{2}\ &=0.5\\ \frac{1}{3}\ &=0.(3)\\ \frac{1}{4}\ &=0.25\\ \frac{1}{5}\ &=0.2\\ \frac{1}{6}\ &=0.1(6)\\ \frac{1}{7}\ &=0.(142857)\\ \frac{1}{8}\ &=0.125\\ \frac{1}{9}\ &=0.(1)\\ \frac{1}{10}&=0.1 \end{align} \]
Where \( 0 \).\( 1 \)(\( 6 \)) means \( 0 \).\( 166666... \), and has a \( 1 \)-digit recurring cycle. It can be seen that \( \frac{1}{7} \) has a \( 6 \)-digit recurring cycle.
Find the value of \( d \) \( <1000 \) for which \( \frac{1}{d} \) contains the longest recurring cycle in its decimal fraction part.
Brute force
How do you find the decimals of a fraction?
In elementary school, we learned a method to convert fractions to decimals. Repeat the process of multiplying the numerator by 10:
- The next numerator is the rest of the Euclidean division by the denominator.
- The quotient is the next decimal.
For example with \( \frac{1}{7} \):
\[ \begin{align} \frac{1}{7} &= 7 * \mathbf{0} + 1\\ \frac{10}{7} &= 7 * \mathbf{1} + 3\\ \frac{30}{7} &= 7 * \mathbf{4} + 2\\ \frac{20}{7} &= 7 * \mathbf{2} + 6\\ \frac{60}{7} &= 7 * \mathbf{8} + 4\\ \frac{40}{7} &= 7 * \mathbf{5} + 5\\ \frac{50}{7} &= 7 * \mathbf{7} + 1\\ \frac{10}{7} &= \dots\\ \end {align} \]
That give us \( \frac{1}{7} = 0,142857... \).
We just have to pay attention to some special cases:
- When the rest is 0, the division is finite and there is no cycle. We can assume that the length of the cycle is 0.
- The length of the cycle is not the number of time we repeat the process of finding the decimals of a fraction. For example with \( \frac{1}{6} = 0, 166... \) the cycle is 1. But there is some leading number before it.
Detecting the cycle is possible using a set. But we will have no way of knowing when it started, which is required to find its length. We need to store both the numbers and their positions for every decimal. When a duplicate is found, it is enough to calculate the length between the old and the newly found duplicate. Rather than a set, using a dictionary whose key is the rest and value its position in the decimal form of the fraction will solve both problem.
def find_cycle(n):
rest = 1
seen = {}
for i in itertools.count(0):
if rest == 0:
return 0
if rest in seen:
return i - seen[rest]
seen[rest] = i
rest = (rest * 10) % n
The last step is to test all numbers below 1000 and find the one with the greatest cycle.
def reciprocal_cycles(n=1000):
return max(((find_cycle(i), i) for i in range(2, n)))[1]
Carmichael function
The Brute force solution works and is not that slow. Yet, with a few observations, we can improve it.
- If you played a bit with the previous snippet of code, you might have notice that most of the duplicate digits are 1. That's not a coincidence, the first rest is also 1. In fact, what we are searching for is more known as the result of the Carmichael function:
The Carmichael function associates to every positive interger \( n \) a positive integer \lambda{n}, defined as the smallest positive integer \( m \) such that \[ a^m \equiv 1\ [ n ] \]
In our case, \( a \) is always 10 and \( m \) is the length of the cycle we are searching for the number \( n \).
Knowing that, we can try to make some observations:
-
Let \( f=\frac{1}{2^{a} 5^{b}} \), where \( a,b\in\mathbb{Z}_{\geqslant 0} \). f has a finite and non-recurring decimal representation. Proof on Wikipedia .
-
If \( \frac{1}{m} \) is a repeating decimal and \( \frac{1}{n} \) is a terminating decimal, them \( \frac{1}{mn} \) has a nonperiodic part whose length is that of \( \frac{1}{n} \) and a repeating part whose length is that of \( \frac {1}{m} \). From Wolfram MathWorld
-
The recurring part of \( \frac{1}{d} \) cannot have more than \( d - 1 \) digits. Proof on Wikipedia
Let's try to use this information in our program:
We can reduce \( n \) by dividing it with \( 2 \) or \( 5 \) until it become coprime with \( 10 \) (3). If after this reduction \( n = 1 \), \( \frac{1}{n} \) has no recurring part (2).
We do not need to use a dictionary to find our cycle. Since \( n \) will be coprime with 10, there will not be any leading number before the recurring part (4). We know that if the rest is 1, we found our cycle (1).
def find_cycle(n):
while n % 2 == 0:
n /= 2
while n % 5 == 0:
n /= 5
if n == 1:
return 0
i = 1
r = 10
while r != 1:
r = (r * 10) % n
i += 1
return i
We can start from 1000 and iterate until \( \frac{n}{2} \) (2). If we find \( n \) such that \( \lambda{n} == n - 1 \), there will be no point to go any further (4).
def reciprocal_cycles(n=1000):
max_cycle = 0
res = 0
for i in range(n, n // 2, -1):
current_cycle = find_cycle(i)
if current_cycle == i - 1:
return i
if current_cycle > max_cycle:
max_cycle = current_cycle
res = i
return res
Solution
983
Quadratic primes
Euler discovered the remarkable quadratic formula:
\[ n^2 + n + 41 \]
It turns out that the formula will produce \( 40 \) primes for the consecutive integer values \( 0 \leq n \leq 39 \). However, when \( n=40 \), \( 40^2+40+41=40(40+1)+41 \) is divisible by \( 41 \), and certainly when \( n=41 \), \( 41^2+41+41 \) is clearly divisible by \( 41 \).
The incredible formula \( n^2-79n+1601 \) was discovered, which produces \( 80 \) primes for the consecutive values \( 0 \leq n \leq 79 \). The product of the coefficients, \( −79 \) and \( 1601 \), is \( −126479 \).
Considering quadratics of the form:
\[ \begin{align} & n^2 + an + b,\ where\ |a|< 1000\ and\ |b|\ \leq 1000\\ \\ & where\ |n|\ is\ the\ modulus/absolute value\ of\ n\\ & e.g.\ |11|=11\ and\ |-4|=4 \end{align} \]
Find the product of the coefficients, \( a \) and \( b \), for the quadratic expression that produces the maximum number of primes for consecutive values of \( n \), starting with \( n=0 \).
Brute force
The problem is to find the best combination of \( a \) and \( b \) such that the formula:
\[ n^2 + an + b \]
produces the largest number of primes for consecutive values of \( n \). The absolute value of \( a \) and \( b \) must be less than \( 1000 \).
The brute force solution is to iterate from \( -1000 \) to \( 1000 \) for \( a \) and \( b \) and count the number of consecutive primes each time.
def quadratic_primes(limit=1000):
res = 0
max_primes = 0
for a in range(-limit, limit):
for b in range(-limit, limit):
n = 0
while isprime(n ** 2 + a * n + b):
n += 1
if n > max_primes:
max_primes = n
res = a * b
return res
Shorten the intervals
If with take a closer look at the equation, we should find useful information. For example, with some peculiar values of \( n \), we can narrow down the ranges of \( a \) and \( b \).
We are searching \( p \) prime such that:
\[ p = n^2 + an + b \]
For \( n = 0\), the equation is \( p = b \). That means that \( b \) must be a prime.
For \( n = b \), the equation is \( p = b^2 + ab + b = b(b + a + 1) \) which is divisible by \( b \). \( b \) is in fact the limit of consecutive primes that can be found using this equation.
Rearranging the equation we have:
\[ p = n^2 + an + b \Leftrightarrow p - b = n(n + a) \]
Since both \( p \) and \( b \) are prime, \( p - b \) is an even number.
If \( n \) is even then \( n(n + a) \) will also be even.
If \( n \) is odd, then \( n(n + a) \) will be odd only if \( a \) is odd.
For \( n = 1 \), \( n^2 + an + b \) will never be a prime if \( a \) is even.
All this information can help quite a bit:
- \( a \) must be an odd number between.
- b must be a prime.
- b is the upper limit of consecutive primes.
def quadratic_primes():
primes_b = list((primerange(0, 1000)))[::-1] # b is prime.
res = 0
max_primes = 0
for a in range(-999, 1000, 2): # a is odd.
for b in primes_b:
if b < max_primes: # b is the limit for consecutive prime.
continue
n = 0
while isprime(n ** 2 + a * n + b):
n += 1
if n > max_primes:
max_primes = n
res = a * b
return res
Lucky numbers of Euler
Thanks to mathworld , we know that if \( p(n) = n^2 + n + 41 \) is prime-generating for \( 0 \leq n \leq L \), then so is \( p(L - n) \).
\[ \begin{align} &p(n) = n^2 + n + 41\\ &p(L - n) = (L - n)^2 + L - n + 41\\ &p(L - n) = L^2 - 2Ln + n^2 + L - n + 41\\ &p(L - n) = n^2 - (2L + 1)n + L^2 + L + 41\\ &p(L - n) = n^2 - (2L + 1)n + p(L)\\ &p(L - n) = n^2 + an + b\\ &where\ a = -(2L + 1)\ and\ b = L^2 + L + 41\\ \end{align} \]
We also know from the Shorten the intervals solution that when \( n = 0 \), \( b = L^2 + L + 41 \) is prime. Since \( |b| < 1000 \) we have:
\[ b = L^2 + L + 41 < 1000 \Rightarrow -31 \leq L \leq 31 \]
We also know that \( b \) is the upper limit of consecutive primes, it means that \( b \) must be the largest number possible. It corresponds to \( L = 30 \) and \( b = 30^2 + 30 + 41 = 971 \) and \( a = -(2 \times 30 + 1) = -61 \).
We can find a general solution based on the limit by searching the value of \( L \) and then computing \( a \times b = (L^2 + L + 41) \times (-2(L + 1)) \).
The value of \( L \) is the largest solution for \( L^2 + L + 41 < limit \)
.
We have \( \Delta = 1 - 4(41 - limit) \), thus the solution is L =
\( \left\lfloor \frac{-1 + \sqrt{4(41 - limit)}}{2} \right\rfloor \)
def quadratic_primes(limit=1000):
l = floor((-1 + sqrt(1 - 4 * (41 - limit))) / 2)
return (l ** 2 + l + 41) * (-(2 * l + 1))
Solution
-59231
Number spiral diagonals
Starting with the number \( 1 \) and moving to the right in a clockwise direction a \( 5 \) by \( 5 \) spiral is formed as follows:
\[ \begin{gather} \color{red}{21}\ 22\ 23\ 24\ \color{red}{25}\\ 20\ \ \ \color{red}{7}\ \ \ 8\ \ \ \color{red}{9}\ 10\\ 19\ \ \ 6\ \ \ \color{red}{1}\ \ \ 2\ 11\\ 18\ \ \ \color{red}{5}\ \ \ 4\ \ \ \color{red}{3}\ 12\\ \color{red}{17}\ 16\ 15\ 14\ \color{red}{13}\\ \end{gather} \]
It can be verified that the sum of the numbers on the diagonals is \( 101 \).
What is the sum of the numbers on the diagonals in a \( 1001 \) by \( 1001 \) spiral formed in the same way?
Brute force
This problem actually contains two problem. The first is the spiral creation problem and the second is the diagonal sum problem.
The direction of the spiral is a cycle of 'EAST', 'SOUTH', 'WEST' and 'NORTH' but the main question is to know when it changes.
There is many ways of creating a spiral matrix, but the idea I had was to insert number in every cell in the same direction until the cell in the next direction is empty.
Once the spiral matrix is created, we can compute the diagonal using the
trace function of numpy. We also need to remove the cell in the middle because
it will be counted twice.
def number_spiral_diagonals(n=1001):
dir = [(0, 1), (1, 0), (0, -1), (-1, 0)] # EAST, SOUTH, WEST, NORTH
cur_dir = 0
(x, y) = (n // 2, n // 2) # Center of the matrix
spiral = np.zeros(n * n, dtype=int).reshape(n, n)
spiral[x, y] = 1
for i in range(2, n * n + 1):
# Move along the current direction and update the new cell
dx, dy = dir[cur_dir]
x, y = x + dx, y + dy
spiral[x, y] = i
# If the cell in the next direction is empty: change direction
dx, dy = dir[(cur_dir + 1) % 4]
if spiral[x + dx, y + dy] == 0:
cur_dir = (cur_dir + 1) % 4
return np.trace(spiral) + np.trace(np.fliplr(spiral)) - 1
Summation
The sum of the diagonals is actually the sum of the 4 corners of each subcube of the spiral matrix.
With:
\[ \begin{gather} \color{red}{21}\ 22\ 23\ 24\ \color{red}{25}\\ 20\ \ \ \color{red}{7}\ \ \ 8\ \ \ \color{red}{9}\ 10\\ 19\ \ \ 6\ \ \ \color{red}{1}\ \ \ 2\ 11\\ 18\ \ \ \color{red}{5}\ \ \ 4\ \ \ \color{red}{3}\ 12\\ \color{red}{17}\ 16\ 15\ 14\ \color{red}{13}\\ \end{gather} \]
The sum is \( (1) + (3 + 5 + 7 + 9) + (13 + 17 + 21 + 25) \)
For an \( n \times n \) grid, with n being odd, the top right corner is \( n^ 2 \), the top left corner is \( n^2 -n + 1 \), the bottom left corner is \( n^2 -2n + 2 \) and the bottom right corner is \( n^2 -3n + 3 \). The sum of these corners is \( 4n^2 -6n + 6 \).
We need to sum these corners for all odd \( n \) between 3 and \( l \). Odd numbers can be written in the form \( 2k + 1 \). By replacing \( n \) with \( 2k + 1 \) we have:
\[ 4n^2 -6n + 6 = 4(2k+1)^2 -6(2k+1) + 6 = 16k^2 + 4k + 4 \]
The sum become:
\[ \begin{align} S &= \sum _{k=1}^{m} 16k^{2} + 4k + 4\\ S &= 16\sum _{k=1}^ {m} k^{2} + 4\sum _{k=1}^{m} k + 4\sum _{k=1}^{m} 1\\ S &= \frac{16m(m+1) (2m+1)}{6} + \frac{4m(m + 1)}{2} + 4m\\ S &= \frac{16m^3}{3} + 10m^2 + \frac{26m}{3}\\ \end{align} \]
where \( m = \frac{l - 1}{2} \)
This sum plus \( 1 \) (the center of the spiral matrix) is the solution we are searching for:
def number_spiral_diagonals(n=1001):
m = (n - 1) // 2
return int(1 + (16 / 3) * m ** 3 + 10 * m ** 2 + (26 / 3) * m)
Solution
669171001
Distinct powers
Consider all integer combinations of \( a^b \) for \( 2 ≤ a ≤ 5 \) and \( 2 ≤ b ≤ 5 \):
\[ \begin{align} &2^2=4, 2^3=8, 2^4=16, 2^5=32\\ &3^2=9, 3^3=27, 3^4=81, 3^5=243\\ &4^2=16, 4^3=64, 4^4=256, 4^5=1024\\ &5^2=25, 5^3=125, 5^4=625, 5^5=3125\\ \end{align} \]
If they are then placed in numerical order, with any repeats removed, we get the following sequence of \( 15 \) distinct terms:
\[ 4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125 \]
How many distinct terms are in the sequence generated by \( a^b \) for \( 2 ≤ a ≤ 100 \) and \( 2 ≤ b ≤ 100 \)?
Brute force
Using python's {} set comprehension we can create a set with all the terms generated by the sequence: \( a^b \). Since a set discards duplicate elements, the solution is the length of that set.
def distinct_powers(n=100):
return len({a ** b for a in range(2, n + 1) for b in range(2, n + 1)})
Discarding duplicate
We can actually solve this problem with pen and paper.
I won't explain the solution since jorgbrown has already done a great job in
his post:
Suppose \( a \) is a perfect square of the smaller \( a \), but not a square of a square. Then we have a duplicate when \( b \) is \( 2, 3, 4\dots \) up to \( 50 \). That is, \( 49 \) duplicates.
Suppose \( a \) is a perfect cube of a smaller \( a \). When \( b \) is \( 2 \) through \( 33 \), we have duplicates of smaller \( a \) raised to the power \( b\times3 \). When \( b \) is \( 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66 \), we have duplicates of a smaller \( a \) raised to the power \( (\frac{b}{2})\times3 \). Total is \( 32 + 17 \), or again, \( 49 \) duplicates.
Suppose \( a \) is the square of the square of a smaller \( a \). When \( b \) is \( 2 \) through \( 49 \), we have duplicates of the square root of a raised to the power \( (b\times2) \).
When \( b \) is \( 51, 54, 57, 60, 63, 66, 69, 72, \) or \( 75, \) we have dupes of \( a^{(\frac{3}{4})} \) raised to the power \( \frac {b\times4} {3} \). Total is \( 49 + 9 \), or \( 58 \).Suppose \( a \) is the fifth power of a smaller \( a \). We have dupes of fifth root of a raised to the power \( (b\times5) \), which covers \( b \) from \( 2 \) to \( 20 \). Then we have dupes of \( a^{(\frac{2}{5})} \) raised to the power \( \frac{b\times5}{2} \), which covers \( b \) of \( 22, 24, 26, 28, 30, 32, 34, 36, 38, 40 \). Then we have dupes of \( a^{(\frac{3}{5})} \) raised to the power \( \frac{b\times5}{3} \), which covers \( b \) of \( 21, 27, 33, 39, 42, 45, 48, 51, 54, 57, 60 \). Last, we have dupes of \( a^\frac{4}{5} \) raised to the power \( \frac{b\times5}{4} \), which covers \( b \) of \( 44, 52, 56, 64, 68, 72, 76\), and \( 80 \). Total dupes: \( 48 \).
And the last power we have to worry about is \( 6 \). We have dupes of the square root of a raised to power \( (b\times2) \), which covers \( b \) from \( 2 \) to \( 50 \). Then we have dupes of the sixth root to the power \( \frac{b\times6}{4} \), which covers \( b \) of \( 52 \), \( 54, 56, 58, 60, 62, 64, 66 \). And last we have dupes of the sixth root to the power \( \frac{b\times6}{5} \), which covers \( b \) of \( 55, 65, 70, 75 \), and \( 80 \). Total dupes: \( 62 \).
Now let's put it all together:
squares: \( 4, 9, 25, 36, 49, 100 \): These \( 6 \) squares have \( 49 \) dupes each, \( 6 \times 49 \) = \( 294 \)
cubes: \( 8, 27 \): These \( 3 \) cubes have \( 49 \) duplicates each: \( 2 \times 49 = 98 \)
4th power: \( 16, 81 \). These \( 2 \) have \( 58 \) dupes each: \( 2 \times 58 = 116 \)
5th power: \( 32 \). This has \( 48 \) dupes.
6th power: \( 64 \): this has \( 62 \) dupes.
Total # dupes: \( 618 \). \( 9801-618 \) is \( 9183 \).
Solution
9183
Digit fifth powers
Surprisingly there are only three numbers that can be written as the sum of fourth powers of their digits:
\[ \begin{align} 1634 = 1^4 + 6^4 + 3^4 + 4^4\\ 8208 = 8^4 + 2^4 + 0^4 + 8^4\\ 9474 = 9^4 + 4^4 + 7^4 + 4^4 \end{align} \]
As \( 1=1^{4} \) is not a sum it is not included.
The sum of these numbers is \( 1634+8208+9474=19316 \).
Find the sum of all the numbers that can be written as the sum of fifth powers of their digits.
Brute force
Finding number that can be written as the sum of fifth powers of theirs digits is easy. The main difficulty of this problem is to find an upper bound and thus to know when to stop the iteration.
The sum of the fifth powers of a \( n \)-digits number will always be less than or equal to \( n * 9^5 \). We need to find \( n \) such that \( n * 9^5 < 10^n - 1 \) for all \( n \). The solution is actually very complex, but with \( n = 5 \) we have \( 5 * 9^5 = 295245 > 10^5 - 1 \) and with \( n = 6 \) we have \( 6 * 9^5 = 354294 < 10^6 - 1 \). Which implies that it is pointless to try any number with more than 6 digits.
def digit_fifth_powers():
return sum((n for n in range(2, 999999)
if sum(int(i) ** 5 for i in str(n)) == n))
Search unique combination
There is no need to try all numbers with at most 6 digits. What is really important is to try all combinations of numbers with at most 6 digits. For example, the sum of the fourth powers of digits of \( 1346 \) is the same as the sum of \( 1634, 1436\dots \) But even if the sum is the same for \( 1356 \) and \( 1634 \), only \( 1634 \) has a sum equal to itself. So how can we avoid calculating duplicate combinations but still find the solution ?
We need to build a list of these combinations, which is easily done with a recursive function. The idea is to create the string so that the digits are sorted. The stopping condition is the number of digits. Recursive functions are a pain to understand, but if you print the result and the string after each iteration, you should understand the function without too much trouble.
I used yield instead of building an entire list, but you can consider that
it's the same thing.
def build_combination(d, n=0, s=''):
if d == 0:
yield s
else:
for i in range(n, 10):
for v in build_combination(d - 1, i, s + str(i)):
yield v
The trick is to compute the sum a first time, for example, taking \( 1346 \) which sum is equal to \( 1^5 + 3^5 + 4^5 + 6^5 = 1634 \). Then, repeat the operation a second time \( 1^5 + 6^5 + 3^5 + 4^5 = 1634 \). If the total is the same for both computations, then you have found one combination that works.
Instead of computing the fifth power of each digit, we can compute them once and
store them in a cache. The rest is just trying all the previously found
combinations. We need to remove 1 from the final result as the problem
indicates.
def digit_fifth_powers():
cache = [i ** 5 for i in range(0, 10)]
res = 0
for n in build_combination(6):
total = sum(cache[int(c)] for c in n)
if sum(cache[int(c)] for c in str(total)) == total:
res += total
return res - 1
Solution
443839
Coin sums
In the United Kingdom the currency is made up of pound (£) and pence (p). There are eight coins in general circulation:
\[ \begin{align} 1p,\ 2p,\ 5p,\ 10p,\ 20p,\ 50p,\ £1\ (100p),\ and £2\ (200p). \end{align} \]
It is possible to make £\( 2 \) in the following way:
\[ \begin{align} 1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p\end{align} \]
How many different ways can £\( 2 \) be made using any number of coins?
Brute force
We are searching for all the combination to make 2 pounds using the eights following coins in pence:
1, 2, 5, 10, 20, 50, 100, 200.
Combination implies that making 2 pounds with 100 + 50 + 50 pences is the same
as 50 + 100 + 50 pences. To avoid this, we will try every piece one by one in
increasing order.
The algorithm will use an accumulator that will increase with each iteration of the function:
- If the accumulator reaches 200, a combination has been found.
- If the accumulator is greater than 200 the current combination will not work.
- If the accumulator is less than 200, add a new piece. To avoid duplicate combinations, always add piece larger than or equal to the last one.
From solution1.py:
def coin_sums(n=200):
coins = [1, 2, 5, 10, 20, 50, 100, 200]
def coin_sums_rec(accumulator, minimum_piece):
if accumulator == n:
return 1
if accumulator > n:
return 0
return sum(
coin_sums_rec(accumulator + coins[new_piece], new_piece) for new_piece in range(minimum_piece, len(coins))
)
return coin_sums_rec(0, 0)
Dynamic programming
The last solution does not scale to the number of parts or the target. We can do better using dynamic programming, but first, we must divide the problem into subproblems.
Let's start with the ways to do 1p using all the pieces we have. The table is a cumulative sum, so the value of each cell is the number of ways to have the target using the pieces up to the current one. We consider that there is only one way to do 0p, so the first column is always 1.
| 1 | \( \leq \)2 | \( \leq \)5 | \( \leq \)10 | \( \leq \)20 | \( \leq \)50 | \( \leq \)100 | \( \leq \)200 | |
|---|---|---|---|---|---|---|---|---|
| 0p | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1p | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
This table means that there is only one way to express 1p, no matter what coins we are using.
| 1 | \( \leq \)2 | \( \leq \)5 | \( \leq \)10 | \( \leq \)20 | \( \leq \)50 | \( \leq \)100 | \( \leq \)200 | |
|---|---|---|---|---|---|---|---|---|
| 0p | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1p | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2p | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
2p can be expressed using 1p: 1p + 1p, but also using 2p. With the other coins the result remain the same.
| 1 | \( \leq \)2 | \( \leq \)5 | \( \leq \)10 | \( \leq \)20 | \( \leq \)50 | \( \leq \)100 | \( \leq \)200 | |
|---|---|---|---|---|---|---|---|---|
| 0p | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1p | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2p | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 3p | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 4p | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 5p | 1 | 3 | 4 | 4 | 4 | 4 | 4 | 4 |
You might start to understand how this table was computed:
- The first column is always 1, there is only one way to express any target with 1p.
- The first row is always 1, there is only one way to express 0p.
- For the rest we construct the table lines by lines, the current cells is the
sum of two possibilities:
- The new coin is not used,
- The new coin is not used: the number of ways to make \( n \) is the number of way to make \(n - 1 \) using the same coins, which is the value in the left cell.
- If possible, the new coin is used: the number of ways to make \( n \) is the number of ways to make \( n - c \) using the same coins, which is the value in the cell on the same column but on the line \( n - c \).
For example with the last line, the first column is obviously 1 and the second is: 1 (left cell) + 2 (the number of ways to make \( 5p - 2p = 3p \), above cell).
So, using a cache table, we can drop the time complexity from \( O(m^n) \) to \( O(nm) \), where \( n \) is the target and \( m \) the number of coins. But we now have an \( O(nm) \) space complexity.
From solution2.py:
def coin_sums(n=200):
coins = [1, 2, 5, 10, 20, 50, 100, 200]
cache = [[1] + [0] * (len(coins) - 1) for _ in range(n + 1)]
for i in range(n + 1):
for j in range(1, len(coins)):
cache[i][j] = cache[i][j - 1]
if coins[j] <= i:
cache[i][j] += cache[i - coins[j]][j]
return cache[-1][-1]
Better dynamic programming
Dynamic programming can be a bit improved by using a single array instead of a table. The array will contain the number of ways to make \( n \) using the coins we have. The array will be initialized with 1, and we will update it by adding the number of ways to make \( n - c \) to the current value. This way we will only need \( O(n) \) space. The time complexity will be the same as the previous solution, but the space complexity will be better.
From solution3.py:
def coin_sums(n=200):
coins = [1, 2, 5, 10, 20, 50, 100, 200]
cache = [1] + [0] * n
for coin in coins:
for i in range(coin, n + 1):
cache[i] += cache[i - coin]
return cache[-1]
Solution
73682
Pandigital products
We shall say that an \( n \)-digit number is pandigital if it makes use of all the digits \( 1 \) to \( n \) exactly once; for example, the \( 5 \)-digit number, \( 15234 \), is \( 1 \) through \( 5 \) pandigital.
The product \( 7254 \) is unusual, as the identity, \( 39×186=7254 \), containing multiplicand, multiplier, and product is \( 1 \) through \( 9 \) pandigital.
Find the sum of all products whose multiplicand/multiplier/product identity can be written as a \( 1 \) through \( 9 \) pandigital.
HINT: Some products can be obtained in more than one way so be sure to only include it once in your sum.
Brute force
First, we need to know when the multiplicand/multiplier/product triplet is pandigital. There are several ways to do this, probably the most obvious being to convert the triplet to a single sorted string and compare it to "123456789".
From solution1.py:
def is_pandigital(multiplicand, multiplier, product):
return sorted(str(multiplicand) + str(multiplier) + str(product)) == list("123456789")
One solution I really like uses a binary number to keep track of the digits. This is faster than converting the triplet to a string and uses less memory than a set or list. This method uses the bits as flags to check if a digit is present. If one of the digits is used twice, the triplet is not pandigital. If the final binary number is 0b1111111110, the triplet is pandigital.
def is_pandigital3(multiplicand, multiplier, product):
digits = 0
for n in (multiplicand, multiplier, product):
while n:
if digits & (1 << (n % 10)):
return False
digits |= 1 << (n % 10)
n //= 10
return digits == 0b1111111110
Next, we need to find all the possible multiplicand/multiplier/product combinations. We can do this by brute force, trying all the possible values for the multiplicand and multiplier from 1 to 987654321. But the calculation will take too long.
We know that if the multiplier is 5 digits, then the result will be at least 5 digits, so the total number of digits will be at least 11 and therefore not pandigital.
On the contrary, if the multiplier is 1 digit and the multiplicand 3 digits, the result will be 4 digits and the total number of digits will be 8.
Trying different combinations of multiplicand and multiplier, we find that only the following one result in a 9-digit triplet.
- 2 digits * 3 digits = product of 4 or 5 digits
- 1 digit * 4 digits = product of 4 or 5 digits
We can limit the search to these combinations. To avoid duplicates, we can store the current pandigital products in a set and compute the sum at the end.
From solution1.py:
def pandigital_products():
products = set()
for i in range(1, 100):
for j in range(100 if i > 9 else 1000, 10000 // i + 1):
if is_pandigital3(i, j, i * j):
products.add(i * j)
return sum(products)
Solution
45228
Digit cancelling fractions
The fraction \( \frac{49}{98} \) is a curious fraction, as an inexperienced mathematician in attempting to simplify it may incorrectly believe that \( \frac{49}{98}=\frac{4}{8} \), which is correct, is obtained by cancelling the\( 9s \).
We shall consider fractions like, \( \frac{30}{50}=\frac{3}{5} \), to be trivial examples.
There are exactly four non-trivial examples of this type of fraction, less than one in value, and containing two digits in the numerator and denominator.
If the product of these four fractions is given in its lowest common terms, find the value of the denominator.
Brute force
The first step is to identify curious faction, such as \( \frac{49}{98} \). A Curious faction can take one of four forms, which can be expressed as follows:
\[ \frac{ax}{bx} = \frac{a}{b} \Rightarrow \frac{10a + x}{10b + x} = \frac{a}{b} \Rightarrow 10ab + bx = 10ab + ax \Rightarrow x(a - b) = 0 \]
This implies that either \( x = 0 \) or \( a = b \). Both solutions are trivial.
\[ \frac{xa}{xb} = \frac{a}{b} \Rightarrow \frac{10x + a}{10x + b} = \frac{a}{b} \Rightarrow 10bc + ba = 10ax + ab \Rightarrow x(a - b) = 0 \]
This yields the same trivial solutions as the first case.
The only non-trivial solutions are of the form \( \frac{ax}{xb} \) or \( \frac{xa}{bx} \). We simply need to determine whether we are dealing with the first or second case and verify whether the fractions are the same with and without \( x \).
From solution1.py:
def is_curious_fraction(numerator, denominator):
if numerator % 10 == denominator // 10:
return abs((numerator / denominator) - (numerator // 10 / (denominator % 10))) < 0.0000001
elif numerator // 10 == denominator % 10:
return abs((numerator / denominator) - (numerator % 10 / (denominator // 10))) < 0.0000001
return False
To ensure accuracy in the presence of floating-point values, the returned value must be compared to a small value to ensure it is close enough to zero.
The second step is to iterate over every fraction, with the numerator being smaller than the denominator, as all fractions must be smaller than 1.
From solution1.py:
def digit_cancelling_fractions():
final_numerator, final_denominator = 1, 1
for numerator in range(10, 100):
for denominator in range(numerator + 1, 100):
if numerator % 10 == 0 or denominator % 10 == 0:
continue
if is_curious_fraction(numerator, denominator):
final_numerator *= numerator
final_denominator *= denominator
return final_denominator // gcd(final_numerator, final_denominator)
Solution
100
Digit factorials
\( 145 \) is a curious number, as \( 1!+4!+5!=1+24+120=145 \).
Find the sum of all numbers which are equal to the sum of the factorial of their digits.
Note: As \( 1!=1 \) and \( 2!=2 \) are not sums they are not included.
Brute force
To identify curious numbers, we first need to iterate over each digit of the number and calculate the factorial of each digit. Then, we need to sum all the factorials and compare the result with the original number. If the sum is equal to the original number, then we have found a curious number.
To speed up the process, we can precompute the factorials and iterate over all digits using Python's string.
From solution1.py:
def is_criterion(x):
facts = [1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
return x == sum(facts[int(i)] for i in str(x))
The next step is to iterate over all numbers and find curious numbers, but we need to find an upper bound. If we take a number \( x \) with \( d \) digits, we have \( 10^{d-1} \leq x < 10^d \). If \( x \) is the equal to the sum of factorials of its digits, then with \( x_i \) being the ith digit of \( x \), we have \( x = \sum_{i=1}^d x_i! < d * 9! \).
Thus, we have \( 10^{d-1} \leq x < d * 9! \). With d=8, the equation is wrong. Therefore, our upper bound is \( 7 * 9!\).
From solution1.py:
def digit_factorials():
return sum(i for i in range(3, 7 * 362880) if is_criterion(i))
Solution
40730
Circular primes
The number, \( 197 \), is called a circular prime because all rotations of the digits: \( 197 \), \( 971 \), and \( 719 \), are themselves prime.
There are thirteen such primes below \( 100 \): \( 2 \), \( 3 \), \( 5 \), \( 7 \), \( 11 \), \( 13 \), \( 17 \), \( 31 \), \( 37 \), \( 71 \), \( 73 \), \( 79 \), and \( 97 \).
How many circular primes are there below one million?
Brute force
Determining whether a number is a circular prime can be achieved by rotating the digits of the number with Python's string slicing functionality, followed by a check for primality. Instead of a loop, we used the built-in function all to check whether all rotations of the number are prime.
From solution1.py:
def is_circular_prime(n):
return all(isprime(int(n[i:] + n[:i])) for i in range(len(n)))
The solution is then a simple sum of all numbers below one million that are circular primes.
From solution1.py:
def circular_primes():
return sum(is_circular_prime(str(i)) for i in range(2, 1000000))
1, 3, 7, 9
It is possible to reduce the number of candidate numbers that need to be checked for circular primality by taking into account that prime numbers cannot end with the digits 0, 2, 4, 5, 6 or 8. Therefore, numbers containing these digits can be skipped from consideration.
By using the itertools.product, it is possible to generate all possible combinations of the digits 1, 3, 7 and 9. This approach reduces the number of potential circular prime to less than 6,000, rather than the previous 1,000,000.
From solution2.py:
def circular_primes():
res = 4
for number_digits in range(2, 7):
for n in itertools.product("1379", repeat=number_digits):
if is_circular_prime("".join(n)):
res += 1
return res
Although the current solution is effective, it's possible to further optimize the solution. For instance, since we check all circular permutations of a given number, we may be checking the same number multiple times. Additionally, we know that all prime numbers can be expressed as either \( 6n+1 \) or \( 6n-1 \). However, implementing these optimizations may not be worthwhile.
Solution
55
Double-base palindromes
The decimal number, \( 585=10010010012 \) (binary), is palindromic in both bases.
Find the sum of all numbers, less than one million, which are palindromic in base \( 10 \) and base \( 2 \).
(Please note that the palindromic number, in either base, may not include leading zeros.)
Brute force
Detecting palindromes with Python's string slicing is easy.
We can use the same approach to detect palindromes in binary form.
Python's bin function returns the binary representation of an integer with a 0b prefix.
If you remove this prefix, we can use the same function to check if the number is a palindrome in binary form.
From solution1.py:
def is_double_palindrome(n):
is_palindrome = lambda s: s == s[::-1]
return is_palindrome(str(n)) and is_palindrome(bin(n)[2:])
To find the solution, we can sum all the number below 1 million that are palindromes in both decimal and binary form.
From solution1.py:
def double_base_palindromes():
return sum(n for n in range(1000000) if is_double_palindrome(n))
Generating palindromes
The Brute force solution iterates over all numbers and check if they are palindromes. We can directly generate palindromes in decimal form and then check if they are palindromic in binary form.
Palindrome are of the form:
abccbaabcbaabbaabaaaa
To generate these, we can create the left half of the palindrome and then mirror it to get the full palindrome.
We just have to be careful with the even and odd cases, like abba and aba.
Because the palindromes limit is 1 million, the left part must be smaller than 1000.
From solution2.py:
def make_palindrome():
left = 1
while left < 1000:
yield int(str(left) + str(left)[::-1][1:]) # Odd length palindromes
yield int(str(left) + str(left)[::-1]) # Even length palindromes
left += 1
The final solution just need to check palindromes in their binary form.
From solution2.py:
def double_base_palindromes():
return sum(n for n in make_palindrome() if is_bin_palindrome(n))
Solution
872187
Truncatable primes
The number \( 3797 \) has an interesting property. Being prime itself, it is possible to continuously remove digits from left to right, and remain prime at each stage: \( 3797 \), \( 797 \), \( 97 \), and \( 7 \). Similarly we can work from right to left: \( 3797 \), \( 379 \), \( 37 \), and \( 3 \).
Find the sum of the only eleven primes that are both truncatable from left to right and right to left.
NOTE: \( 2 \), \( 3 \), \( 5 \), and \( 7 \) are not considered to be truncatable primes.
Brute force
To solve the problem of finding truncatable primes, we will use Python's slicing again to check whether the left and right slices of a number are prime. Using the all function, we can check both slices at once efficiently.
From solution1.py:
def is_truncatable_prime(n):
return all(isprime(int(n[i:])) and isprime(int(n[:i])) for i in range(1, len(n)))
Since the problem states that there are only eleven primes, we don't need to set an upper bound for our iteration. We can use itertools.count to make the code more concise.
From solution1.py:
def truncatable_primes():
res = []
for i in itertools.count(10):
if isprime(i) and is_truncatable_prime(str(i)):
res.append(i)
if len(res) == 11:
return sum(res)
Construct them all
The Brute force solution stops when the eleven primes are found. This is not a very efficient solution. Instead, we can construct all the truncatable primes.
The first digit must be 2, 3, 5 or 7 because the left slice will leave that digit at the end. For the same reason, the last digit must be 2, 3, 5 or 7. Since our solution must have at least 2 digits, the last digit cannot end with 2 or 5, as the right slice will leave a multiple of 2 or 5 at the end.
So the first digit is either 2, 3, 5 or 7 and the last digit is either 3 or 7.
The process is recursive. We will append numbers to the right. It is only possible to add 1, 3, 7 or 9 to the right. In this case we can use 1 or 9 because if it ends in the middle of a number, it won't be a single digit with left or right truncating. Obviously, the number will not be a truncatable prime, but the next iterations might be.
If the number is not a prime, there is no point to continue the recursion. Indeed, if we continue, the right-truncating will end on this number, which is not prime and thus not truncatable. On the contrary, the recursion can be continued until the number is not prime.
By construction, the number is prime and right-truncatable. As explained before, we need to check if it is left-truncatable only if the number ends with 3 or 7. If so, we can add it to the list of truncatable primes.
We will use the keyword yield and yield from to return the results as we find them.
The yield from statement is similar to the yield statement, but it is used to return the results of a generator function.
In a nutshell, we just have to use the sum builtin on the returned values.
From solution2.py:
def construct_truncatable_primes(num):
if isprime(num):
if num > 10 and num % 10 in (3, 7) and is_left_truncatable(str(num)):
yield num
for new_digit in (1, 3, 7, 9):
yield from construct_truncatable_primes(num * 10 + new_digit)
The final solution is just the sum of all the constructed truncatable primes starting with 2, 3, 5 and 7.
From solution2.py:
def truncatable_primes():
return sum(sum(construct_truncatable_primes(d)) for d in (2, 3, 5, 7))
Solution
748317
Pandigital multiples
Take the number \( 192 \) and multiply it by each of \( 1 \), \( 2 \), and \( 3 \):
\[ \begin{align} 192 × 1 = 192\\ 192 × 2 = 384\\ 192 × 3 = 576\end{align} \]
By concatenating each product we get the \( 1 \) to \( 9 \) pandigital, \( 192384576 \). We will call \( 192384576 \) the concatenated product of \( 192 \) and \(( 1 \),\( 2 \),\( 3 )\)
The same can be achieved by starting with \( 9 \) and multiplying by \( 1 \), \( 2 \), \( 3 \), \( 4 \), and \( 5 \), giving the pandigital, \( 918273645 \), which is the concatenated product of \( 9 \) and \(( 1 \),\( 2 \),\( 3 \),\( 4 \),\( 5 )\).
What is the largest \( 1 \) to \( 9 \) pandigital \( 9 \)-digit number that can be formed as the concatenated product of an integer with \(( 1 \),\( 2 \), \( ... \) , \( n )\) where \( n>1 \)?
Brute force
I choose to take one number as a seed, and detect if the product of this seed can form a pandigital number. To do this, you multiply the seed number by increasing numbers until the resulting number is either greater than 9 digits or a pandigital number. Python's string functions make it easy to concatenate numbers, and a set is used to check if a number is pandigital.
From solution1.py:
def is_pandigital_multiples(seed):
digits = str(seed)
for j in itertools.count(2):
digits += str(seed * j)
if len(digits) > 9:
return -1
if len(digits) == 9 and set(digits) == set("123456789"):
return int(digits)
The maximum value for the seed is 10000 because if we multiply 10000 by 1 and 2 and concatenate the results, we get a 10-digit number, which cannot be pandigital. The solution is then given by iterating over every seed and returning the maximum pandigital number found.
From solution1.py:
def pandigital_multiples():
return max(is_pandigital_multiples(seed) for seed in range(1, 10000))
Good old pen and paper
As is often the case with Project Euler problems, the problem can be solved with pen and paper.
Before anything, know that \( [0-9] \) means any digit between \( 0 \) and \( 9 \).
We know that the number to beat is \( 918273645 \), so any solution we find must be greater than that number. We also know that the first multiplier is \( 1 \), so the first digit of our seed must start with \( 9 \). We can discard any number in the form \( 9[0-9], 9[0-9][0-9] \) or any number greater than \( 100000 \), because none of them will result in a 9-digit number when multiplied by (1, 2, 3) or (1, 2, 3, 4).
Therefore, the solution must be of the form \( 9[0-9][0-9][0-9] \).
The solution must contain different digits and no zeros, because of the *1 multiplier. It can not contain any 1 at all because it will be present twice. One with the *1 multiplier and another because the *2 multiplier will result with the number of the form \( 18[0-9][0-9] \).
Therefore, the solution must be of the form \( 9[2-9][2-9][2-9] \).
We can continue these eliminations rules:
\[ \begin{align} &9[5-9][2-9][2-9] * 2 = 19[0-9][0-9][0-9] \text{, the *1 multiplier already contains a 9.}\\ &94[5-9][2-9] * 2 = 189[0-9][0-9] \text{, the *1 multiplier already contains a 9.}\\ &94[2-4][2-9] * 2 = 188[0-9][0-9] \text{, the double 8 is obviously wrong.}\\ &937[2-7] * 2 = 187[0-9][0-9] \text{, the *1 multiplier already contains a 7.}\\ &936[2-7] * 2 = 18724, 18726, 18728, 18730, 18732 \text{ or } 18734 \text{. They always lack the number 5 except for 18730 which have the number 4.}\\ &935[2-7] * 2 = 187[0-1][0-9] \text{, contains either a 0 or a double 1.}\\ &934[2-7] * 2 = 186[8-9][0-9] \text{, contains either a 9 or a double 8.}\\ &933[2-7] \text{ is obviously wrong because of the double 3.}\\ &932[2-6] * 2 = 1864, 1866, 1868, 1870 \text{ or } 1872 \text{. They always lack the number 5 except for 1870 which lack the number 4.}\\ \end{align} \]
Thus, the number must be \( 9327 \). Indeed, \( 9327 + 18654 \) is the number we are looking for.
Solution
932718654
Integer right triangles
If \( p \) is the perimeter of a right angle triangle with integral length sides, \( \{a,b,c\} \), there are exactly three solutions for \( p=120 \).
\( \{20,48,52\}, \{24,45,51\}, \{30,40,50\} \)
For which value of \( p \leq 1000 \), is the number of solutions maximised?
Brute force
The problem actually requires us to find Pythagorean triples with a perimeter of \( p \) less than \( 1000 \). To find the solution for this problem, we can try every possible combination of values for \( \{a,b,c\} \) for every \( p \) and check if \( p = a + b + c \) and \( a^2 + b^2 = c^2 \).
From solution1.py:
def count_pythagorean_triple(p):
count = 0
for a in range(1, p):
for b in range(1, p):
for c in range(1, p):
if a + b + c == p and a * a + b * b == c * c:
count += 1
return count
We want to find the maximum value returned by count_right_triangles but return the \( p \) that corresponds to that value.
We can use the Python max builtin with key equal to our function to get the \( p \) that corresponds to the maximum value returned by count_right_triangles.
From solution1.py:
def integer_right_triangles():
return max(range(1, 1001), key=count_pythagorean_triple)
Fewer loops is better
The Brute force solution is too slow because it tries too many combinations. We should try to reduce the number of possible combinations using the following observations:
- \( 0 < a \leq b < c \) because \( a \) and \( b \) are the shorter sides of the triangle. (1)
- \( c = p - a - b \) because \( a + b + c \) is the perimeter of the triangle. (2)
We can remove one loop thanks to (2), and reduces the number of possible combinations by half thanks to (1). Furthermore, we do not need to check the condition \( p = a + b + c \) because we defined \( c \) using this equation.
From solution2.py:
def count_pythagorean_triple(p):
count = 0
for a in range(1, p):
for b in range(1, a):
c = p - a - b
if a * a + b * b == c * c:
count += 1
return count
Using the equations \( a^2 + b^2 = c^2 \) and \( p = a + b + c \) we can deduct the following:
- If both \( a \) and \( b \) are even, \( c \) will be even, thus \( p \) will be even.
- If both \( a \) and \( b \) are odd, \( c \) will be even, thus \( p \) will be even.
- If one is even and the other is odd, \( c \) will be odd, thus \( p \) will be even.
Therefore, we can reduce the number of possible combinations by only considering \( p \) that are even. The solution to the problem is the maximum number of solutions for \( p \) below \( 1000 \).
The function will be the same as the last one, except that we will only iterate over even values of \( p \).
From solution2.py:
def integer_right_triangles():
return max(range(2, 1001, 2), key=count_pythagorean_triple)
Even fewer loops
The Fewer loops is better solution is still very slow. However, we can make the solution faster by using the equations \( c = p - a - b \) and \( a^2 + b^2 = c^2 \) together.
We can rewrite \( a^2 + b^2 = c^2 \) as \( a^2 + b^2 = (p - a - b)^2 \) and simplify it to \( 2b(p - a) = p(p - 2a) \).
Using this equation, we have \( b = \frac{p(p - 2a)}{2(p - a)} \). We can use this information to remove the loop for \( b \).
Furthermore, \( b \) must be a positive integer and since \( 2(p - a) \) is always positive, \( p - 2a \) must be positive as well. It implies that \( a < 500 \).
Finally, we can iterate over all values of \( a \) less than \( 500 \), and check whether \( p(p - 2a) \) is divisible by \( 2(p - a) \). Summing the number of solutions will give us the number of pythagorean triples for a given \( p \).
From solution3.py:
def count_pythagorean_triple(p):
return sum(p * (p - 2 * a) % (2 * (p - a)) == 0 for a in range(1, p // 2))
The rest is the same as the previous solution.
From solution3.py:
def integer_right_triangles():
return max(range(2, 1001, 2), key=count_pythagorean_triple)
Tree of primitive Pythagorean triples
The Even fewer loops solution is already fast, but we can continue to improve it. Indeed, Pythagorean triples are a generalization of a special case called primitive Pythagorean triples, where \( a \), \( b \) and \( c \) are coprime. There exists multiple ways to generate them, such as the Euclid's formula.
I prefer the Tree of primitive Pythagorean triples method. This method is based on the fact that all primitive Pythagorean triples has the structure of a tree. We start with the root \( (3, 4, 5) \), which is the first primitive pythagorean triples, and then recursively generate the children of each node by multiplying it by a matrix \( A \), \( B \) or \( C \).
\( A \), \( B \) and \( C \) that are defined as: \[ A = \begin{bmatrix} 1 & -2 & 2 \\ 2 & -1 & 2 \\ 2 & -2 & 3 \\ \end{bmatrix}, B = \begin{bmatrix} 1 & 2 & 2 \\ 2 & 1 & 2 \\ 2 & 2 & 3 \\ \end{bmatrix}, C = \begin{bmatrix} -1 & 2 & 2 \\ -2 & 1 & 2 \\ -2 & 2 & 3 \\ \end{bmatrix} \]
In our case we are also interested in the non-primitive Pythagorean triples. To generate these triples, we can start with a primitive Pythagorean triple like \( a,b,c \) and multiply each value by a positive integer. This will create a new triplet \( (k \times a, k \times b, k \times c) \) with perimeter \( p = k \times (a + b + c) \). The limit of this multiplication factor \( k \) is restricted by \( p \) being less than \( 1000 \).
To put it all together, we can write a recursive function that will generate all the primitive Pythagorean triples with perimeter less than \( 1000 \). From there, we can generate all the Pythagorean triples with perimeter less than \( 1000 \). We will use numpy to represent the matrices and perform the multiplication.
From solution4.py:
def compute_all_pythagorean_triples(results, max_p, abc):
curr_p = sum(abc)
if curr_p < max_p:
for perimeter in range(curr_p, max_p, curr_p):
results[perimeter] += 1
compute_all_pythagorean_triples(results, max_p, A @ abc)
compute_all_pythagorean_triples(results, max_p, B @ abc)
compute_all_pythagorean_triples(results, max_p, C @ abc)
Finally, we can count the number of solutions for each perimeter and return the one with the maximum number of solutions.
From solution4.py:
def integer_right_triangles():
results = defaultdict(int)
compute_all_pythagorean_triples(results, 1001, np.array([3, 4, 5]))
return max(results, key=results.get)
Solution
840
Champernowne's constant
An irrational decimal fraction is created by concatenating the positive integers:
\[ 0.12345678910\color{red}{1}112131415161718192021... \]
It can be seen that the \( 12 \)th digit of the fractional part is \( 1 \).
If \( d_n \) represents the nth digit of the fractional part, find the value of the following expression.
\[ d_{1} × d_{10} × d_{100} × d_{1000} × d_{10000} × d_{100000} × d_{1000000} \]
Brute force
The Champernowne constant is a number obtained by concatenating positive integers in decimal form. The simplest way to solve this problem is to create a string with the required 1000000 digits and then extract the ones we need.
In Python, we can use the built-in join method to construct this string easily. This function creates a string which is the concatenation of an iterable ; a range of integers in our case.
The final result is the product of the digits we need. Combining the reduce function from the functools module and the int function with operator.mul, we can get the product of a iterable of integers.
From solution1.py:
def champernownes_constant():
s = "".join(str(i) for i in range(1, 1000000))
print([int(s[10**i - 1]) for i in range(7)])
return reduce(operator.mul, (int(s[10**i - 1]) for i in range(7)))
Foreshadowing
Although the Brute force solution is fast, it will not scale well for larger values and is not an elegant solution. To find a better solution, we need to understand how the champernowne constant is constructed.
For instance, a one-digit number (\(0...9\)) represents \( 9 \) digits in the string. Meanwhile, a two-digit number (\(10...99\)) represents \( 180 \) digits in the string. This is because there are \( 99 - 9 \) number between \( 10 \) and \( 99 \) with each two digits. Thus, their concatenation results in \( 180 \) digits.
By examining the construction of the champernowne constant, we can find a pattern with \( d \) digits:
- \( d = 1 \): \( 1 \times (9 - 0) = 1 \times 9 = 9 \) digits
- \( d = 2 \): \( 2 \times (99 - 9) = 2 \times 90 = 180 \) digits
- \( d = 3 \): \( 3 \times (999 - 99) = 3 \times 900 = 2700 \) digits
- \( d = 4 \): \( 4 \times (9999 - 999) = 4 \times 9000 = 36000 \) digits
We can observ a clear pattern. Specifically, for number with \( d \) digits, the number of digits of the concatenation is \( p(d) = 9d * 10^{d-1} \).
This patten allows us to divide the constant into chunks of digits that correspond to the concatenation of numbers with the same number of digits. For instance:
- The first number with one digit starts at the \( 1^{th} \) digit of the champernowne constant.
- The first number with two digits starts at the \( 1 + 9 = 10^{th} \) digit of the champernowne constant.
- The first number with three digits start at the \( 1 + 9 + 180 = 190^{th} \) digit of the champernowne constant.
To find the first number with \( d \) digits, we just need to sum the number of digits of all numbers with fewer digits. We can define \( s(d) = 1 + \sum_{i=1}^{d-1} p(i) \) as the index of the first number with \( d \) digits in the champernowne constant.
Being able to find the first number with \( d \) digits is very useful. Let's say we want to find \( d(1000) \), we know that \( s(3) = 190 \) and \( s(4) = 2890 \). Thus, \( d(1000) \) is among the numbers with three digits. The first number with three digits is at index \( 190 \), the second at index \( 190 + 3 \), the third at index \( 190 + 6 \) and so on. To generalize, \( d(190 + 3k) \) is the first digit of the \( (100 + k)^{th} \) number. We just need to find the greatest \( k \) such that \( 190 + 3k \leq 1001 \), which is \( k = 270 \). So \( d(190 + 3 \times 270) = d(1000) \) is the first digit of \( 10^{d-1} + k = 100 + 270 = 370 \). Hence \( d(1001) = 7 \).
In summary, to find \( d(n) \), we need to first search in which chunk of digits it lies. This is achieved by finding the largest \( d \) such that \( s(d) \leq n \). Next, we need to find the index of the number that contains \( d(n) \). This is done by finding the largest \( k \) such that \( s(d) + d \times k \leq n \). Finally, we can extract the \( (n - (s(d) + k \times d))^{th} \) digit from this number to obtain \( d(n) \).
From solution2.py:
def d(n):
s = lambda n: 1 + 9 * sum(i * 10 ** (i - 1) for i in range(1, n))
digit = 1
while s(digit) <= n:
digit += 1
digit -= 1
sd = s(digit)
k = floor((n - sd) / digit)
number = str(10 ** (digit - 1) + k)
return int(number[n - (sd + k * digit)])
The final solution is obtained by multiplying the digit with the index of the problem.
From solution2.py:
def champernownes_constant():
return reduce(operator.mul, (d(10**i) for i in range(7)))
Solution
210
Pandigital prime
We shall say that an \( n \)-digit number is pandigital if it makes use of all the digits \( 1 \) to \( n \) exactly once. For example, \( 2143 \) is a \( 4 \)-digit pandigital and is also prime.
What is the largest \( n \)-digit pandigital prime that exists?
Brute force
Based on the definition of a pandigital number, we can deduce that it cannot contain more than 9 digits. Therefore, we can iterate through every permutation of the digits in decreasing order until we find a prime number.
From solution1.py:
def pandigital_prime():
initial = "987654321"
while True:
for s in itertools.permutations(initial):
n = int("".join(s))
if isprime(n):
return n
initial = initial[1:]
Moreover, we can optimize the function slightly by taking into account that the sum of the digits in a 9-digit pandigital number is always 45, which makes it divisible by 3 and hence not prime. The same applies to 8-digit pandigital numbers. Therefore, we can skip these cases and start directly with 7-digit pandigital numbers. However, the overall algorithm remains the same.
Solution
7652413
Coded triangle numbers
The n\( ^{th} \) term of the sequence of triangle numbers is given by, \( t_n=\frac{1}{2}n(n+1) \); so the first ten triangle numbers are:
\[ 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ... \]
By converting each letter in a word to a number corresponding to its alphabetical position and adding these values we form a word value. For example, the word value for SKY is \( 19+11+25=55=t_{10} \). If the word value is a triangle number then we shall call the word a triangle word.
Using words.txt (right click and 'Save Link/Target As...'), a 16K text file containing nearly two-thousand common English words, how many are triangle words?
Brute force
The problem gave us a file with quoted words separated by commas. The first step is to read the file and split the words into a list.
From read_file.py:
def read_file(filename):
with open(filename, "r") as f:
return [word.strip('"') for word in f.read().split(",")]
Subsequently, we need to check if the word is a triangle word. A word is considered a triangle word if the sum of the alphabetical position of its letters is a triangle number. A triangle number is defined by the formula \( \frac{1}{2}n(n+1) \), but we are interested in finding the \( n \) that satisfies this formula. To solve it, we can use the equation:
\[ x = \frac{1}{2}n(n+1) \Rightarrow n^2 + n - 2x = 0 \Rightarrow n = \frac{\pm \sqrt{1 + 8x} - 1}{2} \]
The negative solution \( \frac{- \sqrt{1 + 8x} - 1}{2} \) can be disregarded since we are only interested in positive integers. We can determine if \( x \) is a triangle number by checking if the value of \( \frac{\sqrt{1 + 8x} - 1}{2} \) is an integer. Which can be done easily using the is_integer python function.
From solution1.py:
def is_triangle_number(x):
return (((1 + 8 * x) ** 0.5 - 1) / 2).is_integer()
Finally, we can iterate over each word in the list, calculate its value, and verify if it is a triangle number.
From solution1.py:
def coded_triangle_numbers():
words = read_file("words.txt")
return sum(is_triangle_number(sum(ord(c) - ord("A") + 1 for c in word)) for word in words)
Solution
162
Sub-string divisibility
The number, \( 1406357289 \), is a \( 0 \) to \( 9 \) pandigital number because it is made up of each of the digits \( 0 \) to \( 9 \) in some order, but it also has a rather interesting sub-string divisibility property.
Let \( d_1 \) be the \( 1^{st} \) digit, \( d_2 \) be the \( 2^{nd} \) digit, and so on. In this way, we note the following:
\[ \begin{align} &d_2d_3d_4=406\text{ is divisible by }2\\ &d_3d_4d_5=063\text{ is divisible by }3\\ &d_4d_5d_6=635\text{ is divisible by }5\\ &d_5d_6d_7=357\text{ is divisible by }7\\ &d_6d_7d_8=572\text{ is divisible by }11\\ &d_7d_8d_9=728\text{ is divisible by }13\\ &d_8d_9d_{10}=289\text{ is divisible by }17\\ \end{align} \]
Find the sum of all \( 0 \) to \( 9 \) pandigital numbers with this property.
Brute force
The problem can be split into two parts:
- Check if the permutation satisfies the divisibility property.
- Find all the permutations of the digits \( 0 \) to \( 9 \).
The first part can be done by checking if a particular section of the number is divisible by the corresponding prime number.
From solution1.py:
def is_sub_string_divisible(n):
divisors = [2, 3, 5, 7, 11, 13, 17]
return all(int(str(n)[i + 1 : i + 4]) % d == 0 for i, d in enumerate(divisors))
The second part is done by using the itertools.permutations function. With the caveat that any permutation starting with \( 0 \) should be disregarded.
From solution1.py:
def sub_string_divisibility():
res = 0
for i in itertools.permutations("9876543210"):
if i[0] == "0":
continue
x = int("".join(i))
if is_sub_string_divisible(x):
res += x
return res
It is worth noting that if we encounter a permutation beginning with \( 0 \), we can immediately return the result without further iterations, as all other permutations will also start with \( 0 \).
Generation over iteration
Rather than iterating over all permutations and verifying the divisibility property like the Brute force method, a more efficient solution is to recursively generate permutations that satisfy the divisibility property.
The process begins with all pandigital permutations with 3 digits that are divisible by \( 2 \). Then we can generate all the permutations with 4 digits that are divisible by \( 3 \) by appending the new digits at the end of the previous permutations. We can continue this process until all permutations with 10 digits are generated.
Since the first digit is not important in the divisibility property, it is simpler to start from the end of the number. Thus, we begin with the permutations that are divisible by \( 17 \) and continue adding the remaining digits at the beginning of the previous permutations.
Because the final number cannot start with \( 0 \), we can disregard the permutations that start with \( 0 \) in the final concatenation.
From solution2.py:
def sub_string_divisibility():
digits = "0123456789"
items = [x + y for x in digits for y in digits if x != y] # Permutations of 2 digits
for d in [17, 13, 11, 7, 5, 3, 2]:
items = [
y + x for x in items for y in digits if int((y + x)[:3]) % d == 0 and y not in x
] # Concatenation at the beginning
items = [int(y + x) for x in items for y in digits[1:] if y not in x] # Last concatenation
return sum(items)
With pen and paper
As often with these problems, it is possible to find the solution by hand. The crucial aspect of these solutions is reducing the set of potential solutions.
The \( d_4d_5d_6 \) must be divisible by \( 5 \), thus \( d_6 \) must be \( 0 \) or \( 5 \). If \( d_6 = 0 \), \( 0d_7d_8 \) must be divisible by \( 11 \), which implies that \( d_7 = d_8 \). This is a contradiction since the number is pandigital, thus \( d_6 \) must be \( 5 \).
All the number \( 5d_7d_8 \) that can be divided by \( 17 \) are: \( 506, 517, 528, 539, 550, 561, 572, 583 \) and \( 594 \), but \( 550 \) is not pandigital. Let us now check the number \( d_6d_7d_8 \) that are divisible by \( 13 \), with \( d_6d_7 \) being defined with the above solution:
- \( 06x \Rightarrow x = 5 \), but \( 5 \) is already used.
- \( 17x \) has no solution.
- \( 28x \Rightarrow x = 6\), gives \( 286 \) as a possible solution.
- \( 39x \Rightarrow x = 0 \), gives \( 390 \) as a possible solution.
- \( 61x \Rightarrow x = 1 \), but \( 1 \) is already used.
- \( 72x \Rightarrow x = 8 \), gives \( 728 \) as a possible solution.
- \( 83x \Rightarrow x = 2 \), gives \( 832 \) as a possible solution.
- \( 94x \Rightarrow x = 9 \), but \( 9 \) is already used.
The current only possible solution for \( d_6d_7d_8d_9 \) are \( 5286, 5390, 5728\text{ and }5832 \).
We can continue with the same process for the divisibility by \( 17 \):
- \( 86x \Rightarrow x = 7 \), gives \( 867 \) as a possible solution.
- \( 90x \Rightarrow x = 1 \), gives \( 901 \) as a possible solution.
- \( 28x \Rightarrow x = 9 \), gives \( 289 \) as a possible solution.
- \( 32x \Rightarrow x = 3 \), but \( 3 \) is already used.
The current only possible solution for \( d_6d_7d_8d_9d_{10} \) are \( 52867, 53901\text{ and }57289 \).
We can continue with the same process for the divisibility by \( 7 \):
- \( x52 \Rightarrow x = 2 \) or \( x = 9 \), but \( 2 \) is already used, gives \( 952 \) as a possible solution.
- \( x53 \Rightarrow x = 5 \), but \( 5 \) is already used.
- \( x57 \Rightarrow x = 3 \), gives \( 357 \) as a possible solution.
The current only possible solution for \( d_5d_6d_7d_8d_9d_{10} \) are \( 952867, \text{ and }357289 \).
For \( d_2d_3d_4 \) to be divisible by \( 2 \), \( d_4 \) must be even, with the remaining possible digits being \( 0 \) or \( 4 \) for \( 952867 \) and \( 0, 4 \) or \( 6 \) for \( 357289 \).
Thus, the only possible solutions are for \( d_4d_5d_6d_7d_8d_9d_{10} \) are \( 0952867\), \( 4952867 \), \( 0357289 \), \( 4357289 \), and \( 6357289 \).
The last divisibility property requires \( d_3d_4d_5 \) to be divisible by \( 3 \), which implies that \( d_3 + d_4 + d_5 \) must be divisible by \( 3 \). With the remaining digits, we can check all the possible solutions:
- \( x09 \Rightarrow x = 3 \), gives \( 309 \) as a possible solution.
- \( x49 \) has no solution with the available digit \( 0 \), \( 1 \), or \( 3 \).
- \( x03 \Rightarrow x = 6 \), gives \( 603 \) as a possible solution.
- \( x43 \) has no solution with the available digit \( 0 \), \( 1 \), or \( 6 \).
- \( x63 \Rightarrow x = 0 \), gives \( 063 \) as a possible solution.
The current only possible solution for \( d_3d_4d_5d_6d_7d_8d_9d_{10} \) are \( 30952867 \), \( 60357289 \), and \( 06357289 \). All permutations of these numbers with the remaining digits give a solution that satisfies the divisibility property.
The sum of all this numbers is the solution to the problem.
Solution
16695334890
Pentagon numbers
Pentagonal numbers are generated by the formula, \( P_n=\frac{n(3n−1)}{2} \). The first ten pentagonal numbers are:
\[ 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, ... \]
It can be seen that \( P_4 + P_7 = 22 + 70 = 92 = P_8 \). However, their difference, \( 70 − 22 = 48 \), is not pentagonal.
Find the pair of pentagonal numbers, \( P_j \) and \( P_k \), for which their sum and difference are pentagonal and \( D = |P_k − P_j| \) is minimised; what is the value of \( D \)?
Brute force
The problem can be decomposed into two distinct tasks:
- Verification whether a number is pentagonal or not.
- Determination of the lower bound for the iteration through pentagonal pairs.
The first task can be approached similarly to problem 42, by using the equation \( x = \frac{1}{2}n(3n-1) \) and searching for \( n \).
\[ x = \frac{1}{2}n(3n-1) \Rightarrow 3n^2 - n - 2x = 0 \Rightarrow n = \frac{\pm \sqrt{1 + 24x} + 1}{6} \]
Since we are only concerned with positive integers, the negative solution \( \frac{- \sqrt{1 + 24x} + 1}{6} \) can be disregarded. There, a number is pentagonal if \( \frac{\sqrt{1 + 24x} + 1}{6} \) is an integer.
From solution1.py:
def is_pentagonal(n):
return ((1 + (1 + 24 * n) ** 0.5) / 6).is_integer()
The second task is a bit more tricky since there is no obvious lower bound to terminates the iteration. The only constraints is that that solution \( D \) must be minimal. As the sequence of pentagonal numbers is strictly increasing, at some point, the difference between two successive numbers will exceed the current result. Consequently, the iteration can be stopped, as all subsequent numbers will also surpass the current solution.
The difference between \( P_n \) and \( P_{n+1} \) is: \[ P_{n+1} - P_n = \frac{1}{2}(n+1)(3(n+1)-1) - \frac{1}{2}n(3n-1) = 3n + 1 \]
Hence, the iteration should stop when \( 3n + 1 > D \), which is finite assuming there is a solution.
The approach is to iterate through all pairs of pentagonal numbers \( P_i \) and \( P_j \) with \( j < i \) and verify if both \( P_i + P_j \) and \( P_i - P_j \) are pentagonal. If they are, we have found a solution, and the iteration continues until \( 3 * i + 1 > D \), at which point the current result is the final solution.
To optimize the search, it is more efficient to iterate backwards through \( P_j \) since we are searching for the smallest \( D \) that satisfies the condition. When \( P_i - P_j > D \), the iteration through \( P_j \) can be stopped.
From solution1.py:
def pentagon_numbers():
res = float("inf")
pn = lambda n: n * (3 * n - 1) // 2
for i in itertools.count(2):
if 3 * i + 1 > res:
break
for j in range(i - 1, 0, -1):
a = pn(i)
b = pn(j)
if a - b > res:
break
if is_pentagonal(a + b) and is_pentagonal(a - b) and a - b < res:
res = a - b
return res
Optimal iteration
The main reason the Brute force approach is slow is that the iteration does not increase \( D \) monotonically. For example, the previous solution tries the values of \( D \) in the following order: \( 4 \),\( 7 \),\( 11 \),\( 10 \),\( 17 \),\( 21 \),\( 13 \),\( 23 \),\( 30 \),\( 34 \),\( 16 \)...
Starting with the smallest possible value of \( D \) and increasing it until a solution is found is the optimal iteration approach, as it guarantees the solution with the minimal \( D \). To implement it, we need to iterate through values of \( D \). By definition \( D = P_d = P_i - P_j \) where \( j < i \), it is necessary to determine a method for computing \( i \) and \( j \) from \( d \).
\[ \begin{aligned} P_d &= P_i - P_j\\ &= P_{j+x} - P_{j}\\ &= \frac{6jx +3x^2 - x}{2}\\ &= 3jx + P_x\\ &\Rightarrow j = \frac{P_d - P_x}{3x}\\ \end{aligned} \]
The following can be concluded from the above equation:
- \( j \) must be an integer, so \( P_d > P_x \), thus \( 0 < x < d \) and \( P_d - P_x \equiv 0 \pmod{3x} \).
- \( P_d - P_x = 3(d^2 - x^2) + d - x \Rightarrow x \equiv d \pmod{3} \).
Therefore, we can iterate over every \( d \) and \( x \) such that \( 0 < x < d \) and \( x \equiv d \pmod{3} \). If \( P_d - P_x \equiv 0 \pmod{3x} \), then we can compute \( j \) and \( i = x + j \). By definition, \( P_d \) is pentagonal, so if \( P_i + P_j \) is also pentagonal, then \( D = P_d \) is the solution.
From solution2.py:
def pentagon_numbers():
for d in itertools.count(4):
pd = pn(d)
for x in range(d - 3, 0, -3):
px = pn(x)
if (pd - px) % (3 * x) == 0:
j = (pd - px) // (3 * x)
k = x + j
if is_pentagonal(pn(k) + pn(j)):
return pd
Even better iteration
The Optimal iteration approach is much faster than the Brute force approach. However, for large value of \( d \) the iteration through all the possible \( x \) is still slow. Let's try to add more constraints to reduce the numbers of possibility.
The last solution gave the following equation:
\[ \begin{aligned} P_d & = P_i - P_j\\ \Leftrightarrow d(3d - 1) &= i(3i - 1) - j(3j - 1) \\ &= (i - j)(3(i + j) - 1) \\ \end{aligned} \]
The following can be concluded from the above equation:
- \( i - j \equiv 0 \pmod{d(3d + 1)} \).
- Since \( i \), \( j \), and \( d \) are positive integers, it follows that \( 0 < i - j < d \) because if \( d < i - j \), then \( 3d - 1 < 3(i - j) - 1 < 3(i + j) - 1 \) which implies that \( d(3d - 1) < (i - j)(3i - 3i - 1) \) because \(d, i, j \), a contradiction.
- \( i - j \equiv d \pmod{3} \) because \( 3d - 1 \equiv 3(i + j) - 1 \equiv 2 \pmod{3} \).
To summarize, we are searching for all \( i \) and \( j \) that satisfy: \[ \begin{align} &i\text{ and }j\text{ are positive integers.} \tag{0}\\ &0 < i - j < d \tag{1}\\ &i - j \equiv d \pmod{3} \tag{2}\\ &3(i + j) - 1 \equiv 2 \pmod{3} \tag{3}\\ &i - j \equiv 0 \pmod{d(3d + 1)} \tag{4}\\ \end{align} \]
The solution can be found by iterating through all values of \( d \) and find all divisors \( r_1 = i - j \) that satisfy equation \( 3 \) and \( 4 \).
If \( i = \frac{r_1 + \frac{(r_2 + 1)}{3}}{2} \) is an integer (equation 0), then \( j = i - r_1 \). If both \( P_i \) and \( P_j \) are pentagonal numbers, then the solution is \( P_d \).
It is important to know that this approach is not as efficient as the previous one for small values of \( d \), but it is significantly faster for large values of \( d \), especially if the function for obtaining all the divisors of \( d(3d + 1) \) is optimized.
From solution3.py:
def pentagon_numbers():
pn = lambda n: n * (3 * n - 1) // 2
for d in itertools.count(4):
for r1 in get_divisors(d): # Equation 4
r2 = d * (3 * d - 1) // r1
if r2 % 3 == 2: # Equation 3
i = (r1 + (r2 + 1) // 3) / 2
if i.is_integer(): # Equation 0
j = i - r1
if is_pentagonal(pn(i) + pn(j)):
return pn(d)
It is also worth noting that the pandigital number could be cached, as many of them are computed multiple times.
Solution
5482660
Triangular, pentagonal, and hexagonal
Triangle, pentagonal, and hexagonal numbers are generated by the following formulae:
\[ \begin{align*} &\text{Triangle }&&Tn=\frac{n(n+1)}{2} &&1, 3, 6, 10, 15, ...\\ &\text{Pentagonal }&&Pn=\frac{n(3n−1)}{2} && 1, 5, 12, 22, 35, ...\\ &\text{Hexagonal }&&Hn=n(2n−1) &&1, 6, 15, 28, 45, ...\\ \end{align*} \] It can be verified that \( T_{285} = P_{165} = H_{143} = 40755 \).
Find the next triangle number that is also pentagonal and hexagonal.
Brute force
The brute force approach for solving this problem is straightforward. To start, a function is needed to compute \( T_n \), \( P_n \) and \( H_n \) for a given \( n \).
From solution1.py:
def tn(n):
return n * (n + 1) // 2
From solution1.py:
def pn(n):
return n * (3 * n - 1) // 2
From solution1.py:
def hn(n):
return n * (2 * n - 1)
Then, a while loop can be implemented to iterate until all three numbers are equal. At each iteration, only update one of the two smallest value among \( T_n \), \( P_n \) and \( H_n \). This is because \( T_n \), \( P_n \) and \( H_n \) are all increasing functions of \( n \).
From solution1.py:
def triangular_pentagonal_and_hexagonal():
t, p, h = 286, 166, 144
ti, pi, hi = tn(t), pn(p), hn(h)
while not ti == pi == hi:
if ti < pi:
t += 1
ti = tn(t)
elif pi < hi:
p += 1
pi = pn(p)
else:
h += 1
hi = hn(h)
return ti
Triangular numbers are useless
Let's start by observing the first ten Triangular, pentagonal, and hexagonal numbers:
- Triangular: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...
- Pentagonal: 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, ...
- Hexagonal: 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, ...
It appears that every Hexagonal number is also a Triangular number, specifically \( H_n = T_{2n - 1} \). This relationship is true because \( T_{2n - 1} = \frac{(2n - 1)(2n)}{2} = H_n \). Since every Hexagonal number is also a Triangular number, it's pointless to compute Triangular numbers. Therefore, it is sufficient to iterate through every Hexagonal number and verify if it is also a Pentagonal number.
From solution2.py:
def is_pentagonal(n):
return ((1 + (1 + 24 * n) ** 0.5) / 6).is_integer()
From solution2.py:
def triangular_pentagonal_and_hexagonal():
h = 145
while not is_pentagonal(hn(h)):
h += 1
return hn(h)
Diophantine equations
The Triangular numbers are useless approach exploits the fact that Triangular numbers are useless. Thus, it is sufficient to find \( H_n = T_n \Leftrightarrow 3n^2 - n + 4m^2 - 4m = 0 \). This is known as a Diophantine equation. This problem is very hard to solve in general, so we will use this solver to find the solution.
It gives the following recurrence relation:
\[ x_{n + 1} = 97x_n + 112y_n - 44\\ y_{n + 1} = 84x_n + 97y_n - 38 \]
Starting with the solution \( (n, m) = (1, 1) \), we can easily find the third solution.
From solution3.py:
def triangular_pentagonal_and_hexagonal():
x_n = lambda x_i, y_i: 97 * x_i + 112 * y_i - 44
y_n = lambda x_i, y_i: 84 * x_i + 97 * y_i - 38
x, y = 1, 1
x, y = x_n(x, y), y_n(x, y)
y = y_n(x, y)
return y * (2 * y - 1)
Solution
1533776805
Goldbach's other conjecture
It was proposed by Christian Goldbach that every odd composite number can be written as the sum of a prime and twice a square.
\[ 9 = 7 + 2×1^{2}\\\\ 15 = 7 + 2×2^{2}\\\\ 21 = 3 + 2×3^{2}\\\\ 25 = 7 + 2×3^{2}\\\\ 27 = 19 + 2×2^{2}\\\\ 33 = 31 + 2×1^{2} \]
It turns out that the conjecture was false.
What is the smallest odd composite that cannot be written as the sum of a prime and twice a square?
Brute force
The brute force approach for determining the minimal odd composite number that does not satisfy the Goldbach's other conjecture can be separated into two steps:
- Verify whether a number satisfies the Goldbach's other conjecture.
- Iterate through all odd composite numbers.
The first step can be brute force by iterating through every \( i \leq n \) and verify if \( i \) is prime and \( \sqrt{\frac{n-i}{2}} \) is an integer.
From solution1.py:
def is_odd_goldbach(n):
return any(isprime(i) and (((n - i) / 2) ** 0.5).is_integer() for i in range(1, n + 1))
Assuming the existence of a solution, the second part is straightforward and can be done by iterating through all odd composite numbers until a solution is found.
From solution1.py:
def goldbachs_other_conjecture():
for i in itertools.count(7, 2):
if not is_odd_goldbach(i):
return i
Better iteration and caching
The Brute force approach is fast enough because the solution is small. But the function that determines whether a number satisfies the Goldbach's other conjecture can be further optimized.
The key is to iterate through all double squares \( 2i^2 \) with \( i \leq \sqrt{\frac{n}{2}} \) and check whether \(n - 2i^2 \) is prime. Additionally, a cache of prime numbers can be used and updated when a new prime number is found. New primes can only be found if \( n \) is prime, because \( n - 2i^2 \) prime implies that a previous composite number was prime. Thus, the cache is updated if \( n \) is prime, if not, it can be used to determine whether \( n - 2i^2 \) is prime.
From solution2.py:
def is_odd_goldbach(n, primes_cache):
if isprime(n):
primes_cache.add(n)
return True
return any(n - 2 * i**2 in primes_cache for i in range(1, int(n**0.5) + 1))
The rest stays the same.
From solution2.py:
def goldbachs_other_conjecture():
primes_cache = {2, 3, 5}
for i in itertools.count(7, 2):
if not is_odd_goldbach(i, primes_cache):
return i
Solution
5777
Distinct primes factors
The first two consecutive numbers to have two distinct prime factors are:
\[ 14 = 2 × 7\\\\ 15 = 3 × 5 \]
The first three consecutive numbers to have three distinct prime factors are:
\[ \begin{align} 644 &= 2^2 × 7 × 23\\ 645 &= 3 × 5 × 43\\ 646 &= 2 × 17 × 19. \end{align} \]
Find the first four consecutive integers to have four distinct prime factors each. What is the first of these numbers?
Brute force
To find the first four consecutive integers that possess four distinct prime factors each using a brute force approach can be separated into two steps:
- Find the prime decomposition of a number.
- Iterate over all numbers and check if the next four numbers have four distinct prime factors each.
The prime decomposition has previously been implemented in other problems and, therefore, is not an important component for this approach. To solve this part, the sympy.primefactors function can be used.
The iteration process is straightforward, and the number of distinct primes can be determined using the length of the set of the prime decomposition. To identify the solution, check the next four numbers that have four distinct prime factors each, and return the first number that satisfies this condition.
From solution1.py:
def distinct_primes_factors():
for i in itertools.count(5):
if (
len(set(primefactors(i)))
== len(set(primefactors(i + 1)))
== len(set(primefactors(i + 2)))
== len(set(primefactors(i + 3)))
== 4
):
return i
Cache is life
A clear strategy to enhance the Brute force approach is to cache some results. At each iteration, only the prime decomposition of the current number needs to be computed.
From solution2.py:
def distinct_primes_factors():
cache = [False] * 4
for i in itertools.count(1):
cache[i % 4] = len(set(primefactors(i))) == 4
if all(cache):
return i - 3
Good old Sieve
The Cache is life approach involves computing the prime decomposition of each number, which is a costly operation that can be avoided using a sieve. The downside of this approach is that the sieve requires an arbitrary limit, but it can be increased until the solution is found. Instead of determining which number are primes, the sieve stores the number of distinct prime factors for each number.
The sympy.primefactors function combined multiples algorithm, making its exact complexity difficult to determine. Nevertheless, it is expected to be no more than \( O(sqrt{n}) \), resulting in a previous approach of \( O(n\sqrt{n}) \).
The Sieve of Eratosthenes complexity is \( O(n\log\log{n}) \), which is better than the previous approach. In practive, \( \log\log{n} \) is very small and can be disregarded for simplicity, resulting in a complexity of \( O(n) \).
From solution3.py:
def factors_sieves(n):
factors = [0] * (n + 1)
consecutive = 0
for i in range(2, n + 1):
if factors[i] == 0:
for j in range(2, int(n / i)):
factors[i * j] += 1
consecutive = 0
elif factors[i] == 4:
consecutive += 1
else:
consecutive = 0
if consecutive == 4:
return i - 3
return None
To find the final solution, one can arbitrarily choose a limit and attempt to find a solution. If no solution is found, the limit can be multiplied by two, and the process can be repeated. The complexity of this operation is \( O(1 + 2 + 4 + 8 ... + n) \) which is equal to \( O(2n) \) and equivalent to \( O(n) \).
In theory, this approach should be faster than the previous one, but in practice, it may not be faster for small limits.
From solution3.py:
def distinct_primes_factors():
for i in itertools.count(1):
res = factors_sieves(2**i)
if res is not None:
return res
Solution
134043
Self powers
The series, \( 1^{1}+2^{2}+3^{3}+...+10^{10}=10405071317 \).
Find the last ten digits of the series, \( 1^{1}+2^{2}+3^{3}+...+1000^{1000} \).
Brute force
The naive approach consists of computing the sum of the series and then take the last 10 digits.
From solution1.py:
def self_powers():
return sum(i**i for i in range(1, 1001)) % 10**10
Modulus reduction
The Brute force approach only works thanks to Python's infinite precision integers. In other languages, the result of \( 1000^{1000} \) is too large to be stored in an integer.
Thus, the need of a modulus exponentiation algorithm, which exploits the property that \(a \times b \pmod{m} = [(a \pmod{m}) \times (b \pmod{m})] \pmod{m} \) for any \( m \). Although modulus exponentiation may involve more multiplications than exponentiation followed by modulus, because optimized exponentiation algorithms are better than \( O(n) \). In modulus exponentiation the base is always bound by \( m \), leading to smaller exponentiation and faster computation overall. Consequently, this method reduce both the memory usage, which make it suitable for other languages, and the computation time.
The use of functools.reduce eliminates the need for a loop and is a more efficient and elegant solution.
From solution2.py:
def mod_pow(b, e, mod):
return reduce(lambda acc, _: (acc * b) % mod, range(e), 1)
Similarly, the cumulative sum can also be computed using functools.reduce.
From solution2.py:
def self_powers():
mod = 10**10
sums = (mod_pow(i, i, mod) for i in range(1, 1001))
return reduce(lambda acc, y: (acc + y) % mod, sums)
It is worth mentioning that there exists many optimized techniques for modular exponentiation which can be implemented.
Solution
9110846700
Prime permutations
The arithmetic sequence, \( 1487 \), \( 4817 \), \( 8147 \), in which each of the terms increases by \( 3330 \), is unusual in two ways: (i) each of the three terms are prime, and, (ii) each of the \( 4 \)-digit numbers are permutations of one another.
There are no arithmetic sequences made up of three \( 1 \)-, \( 2 \)-, or \( 3 \)-digit primes, exhibiting this property, but there is one other \( 4 \)-digit increasing sequence.
What \( 12 \)-digit number do you form by concatenating the three terms in this sequence?
Brute force
The brute force approach iterates over all four-digit numbers, \( i \), and all numbers \( j \) until \( i \), \( i + j \) and \( i + 2j \) are primes and permutations of each other. The requirement for the four-digit numbers implies that \(1000 \leq i < 10000 \) and \( i + 2j < 10000 \Rightarrow j < \frac{10000 - i}{2} \).
The permutations condition can be verified by sorting the digits of each number and comparing the sorted strings.
From solution1.py:
def prime_permutations():
for i in range(1000, 10000):
if i == 1487:
continue
for j in range(1, (10000 - i) // 2):
if (
isprime(i)
and isprime(i + j)
and isprime(i + 2 * j)
and sorted(str(i)) == sorted(str(i + j)) == sorted(str(i + 2 * j))
):
return str(i) + str(i + j) + str(i + 2 * j)
Primes permutations
An improvement to the Brute force approach can be made by avoiding the iterations over all numbers. The most restrictive requirements of the problem are that the solution must be four-digit and prime. Fortunately, meeting this condition is really simple as generating the Sieve of Eratosthenes between \( 1000 \) and \( 10000 \) gives a list of all four-digit primes.
The remaining conditions require that the three numbers must be permutations of each other and in arithmetic progression. However, it's difficult to determine all primes that are in arithmetic progression efficiently. As a result, it is better to focus on the permutation requirement. By grouping all primes based on their sorted digits results in lists of four-digit primes with the same permutations.
Finally, the arithmetic constraint can be verified by iterating through each group to find \( p_1 \), \( p_2 \), and \( p_3 \) such that \( p_3 = 2p_2 - p_1 \).
From solution2.py:
def prime_permutations():
primes = list(sieve.primerange(1000, 10000))
primes_permutations = defaultdict(list)
for prime in primes:
primes_permutations["".join(sorted(str(prime)))].append(prime)
for perm in primes_permutations.values():
if len(perm) < 3 or perm[0] == 1487:
continue
for i, p1 in enumerate(perm):
for p2 in perm[i + 1 :]:
p3 = 2 * p2 - p1
if p3 in perm:
return str(p1) + str(p2) + str(p3)
Solution
296962999629
Consecutive prime sum
The prime \( 41 \), can be written as the sum of six consecutive primes:
\[ 41 = 2 + 3 + 5 + 7 + 11 + 13 \]
This is the longest sum of consecutive primes that adds to a prime below one-hundred.
The longest sum of consecutive primes below one-thousand that adds to a prime, contains \( 21 \) terms, and is equal to \( 953 \).
Which prime, below one-million, can be written as the sum of the most consecutive primes?
Brute force
To solve the problem of finding the prime number below one million that can be expressed as the longest sum of consecutive primes, the first idea is to generate all the primes below one million. Subsequently, brute-forcing all possible combinations of consecutive primes can be evaluated to identify the longest sequence whose sum is also a prime.
From solution1.py:
def consecutive_prime_sum(lim=10**6):
primes = list(sieve.primerange(2, lim))
res = 0
max_len = 0
for i in range(len(primes)):
for j in range(i + max_len, len(primes)):
s = sum(primes[i:j])
if s >= lim:
break
if j - i > max_len and s in primes:
max_len = j - i
res = s
return res
Cumulative sum
The Brute force approach has a time complexity of \( O(n^3) \), due to the double loop and the computation of the sum of consecutive primes at each iteration. However, the Sieve of Eratosthenes used for generated the primes has a time complexity of \( O(n\log(\log(n))) \), suggesting that it might be possible to improve the brute force approach.
A major drawback of the brute force approach is the computation of the sum of consecutive primes at each iteration. This can be optimized by using a cumulative sum, which has the additional benefit that the sum of consecutive primes between \( i \) and \( j \) is equal to \( S_j - S_i \), where \( S_i \) is the cumulative sum of the first \( i \) primes. Therefore, searching for the sum of any consecutive primes can be done in constant time.
To effectively iterate over all possible combinations of consecutive primes, it's best to start from the longest possible sequence and then decrease the size of the sequence until a sum is prime. This sequence can be obtained by finding the first cumulative sum that is greater than \( 1000000 \) since it is obvious that the sequence must start from the first prime. Using a binary search this window size can be found in \( O(\log(n)) \).
The remaining step involve iterating over all the possible windows of consecutive primes until a sum is prime. Using a set to store the primes can further improve the time complexity of searching if a sum is prime.
In theory, the time complexity of this approach is \( O(wn) \), where \( w \) is the size of the longest window and \( n \) is the number of primes below \( 1000000 \). Estimating \( w \) based on the size of \( n \) is difficult, but it's clear that it is much smaller than \( n \). For example in our case \( w \) is \( 546 \) and \( n \) is \( 664579 \). In practice, this approach only take a couple of iterations since \( w \) is very small, and the iteration is done starting from the largest window.
From solution2.py:
def consecutive_prime_sum(lim=10**6):
primes = list(sieve.primerange(2, lim))
primes_set = set(primes)
cumul_sum = list(accumulate(primes))
max_window = bisect.bisect_left(cumul_sum, lim)
for window in range(max_window, 0, -1):
for i in range(len(cumul_sum) - window):
s = cumul_sum[i + window] - cumul_sum[i]
if s >= lim:
break
if s in primes_set:
return s
Solution
997651
Prime digit replacements
By replacing the \( 1^{st} \) digit of the \( 2 \)-digit number \( *3 \), it turns out that six of the nine possible values: \( 13 \), \( 23 \), \( 43 \), \( 53 \), \( 73 \), and \( 83 \), are all prime.
By replacing the \( 3 \)rd and \( 4 \)th digits of \( 56 \)*\( * \)3 with the same digit, this \( 5 \)-digit number is the first example having seven primes among the ten generated numbers, yielding the family: \( 56003 \), \( 56113 \), \( 56333 \), \( 56443 \), \( 56663 \), \( 56773 \), and \( 56993 \). Consequently \( 56003 \), being the first member of this family, is the smallest prime with this property.
Find the smallest prime which, by replacing part of the number (not necessarily adjacent digits) with the same digit, is part of an eight prime value family.
Brute force
A straightforward approach to determine the smallest prime that belongs to an eight prime value family involves iterating through all primes and checking whether it is possible to replace \( k \) digits with numbers \( d \) ranging from \( 0 \) to \( 9 \) while still retaining 8 primes. The condition being the difficulty of the problem, can be split into two parts:
- Find all the permutation of digits that should be replaced.
- Replace the digits with numbers ranging from \( 0 \) to \( 9 \) and check whether the resulting number is prime.
The first part can be done quite simply by generating a mask using itertools.product.
The mask is binary list with a length equal to the length of the number to verify, where the value True indicates that the digit at the same index should be replaced.
Although the second part may present some challenges in terms of efficiency, its implementation should remain straightforward since the method is intended to be naive. To solve this, a string of the same length as the original number is constructed, where each digit is selected from either the initial number or the value \( d \), depending on the mask.
Certain corner cases requires some consideration:
- Number starting with \( 0 \) are invalid, otherwise the smallest seven prime value family would start at \( 03 \). Thus any permutation where the first digit is replaced by \( 0 \) should be skipped.
- The mask can not consist of only
Falsevalues, as this would mean that no digit is replaced. Consequently, any permutations with an all-Falsemask should be discarded.
From solution1.py:
def is_nth_prime_value_family(n):
for mask in itertools.product([False, True], repeat=len(n)):
seq_len = 0
res = 0
for d in "0123456789":
if mask[0] and d == "0" or not any(mask):
continue
first = int("".join((d if mask[j] else n[j] for j in range(len(n)))))
if isprime(first):
if seq_len == 0:
res = first
seq_len += 1
if seq_len == 8:
return res
return None
The remaining step simply iterate through all primes and verify whether the number is an eight prime value family. For simplicity, the sympy.sieve functions is used to generate an infinite sequence of primes.
From solution1.py:
def prime_digit_replacements():
for i in sieve:
res = is_nth_prime_value_family(str(i))
if res is not None:
return res
Simple observations
The Brute force approach is very slow and highly inefficient, mainly due to redundant verification. For example, several numbers, such as \( 12345 \) and \( 12346 \), are checked multiples times when the replacement includes the last digit. Therefore, it is necessary to find a better approach to determine which numbers and which replacements are required.
Let's start with some simple observations that can be made to improve the efficiency of the algorithm:
- Since the first number of the sequence must be a prime, there is no need to check numbers lower than the current one during digit replacement. This is because smaller prime are already been verified.
- Since the family is an eight prime value family, at least 8 replacements must be prime. Using 1, it's unnecessary to replace digits greater than \( 2 \), as this would result in fewer than 8 possible replacements.
- Only replacements of \( 3k \) digits, with \( k > 0 \) can give a solution. Let's first remember that a number \( n \) is divisible by \( 3 \) if and only if the sum of its digits is divisible by \( 3 \). The rest modulo \( 3 \) of the sum of the digits of the initial numbers excluding the one that will be replaced is either \( 0 \), \( 1 \) or \( 2 \). If the number of replacements is \( 2 \), then the rest modulo \( 3 \) of the sum of the replacements for \( 0 \) to \( 9 \) is: \( 0 \), \( 2 \), \( 1 \), \( 0 \), \( 2 \), \( 1 \), \( 0 \), \( 2 \), \( 1 \), \( 0 \) respectively. Therefore, whatever the initial number is, the sum of the digits will always be divisible by \( 3 \) at least 3 times, and thus the maximum value family is \( 7 \). The same reasoning can be applied to other non-multiples of \( 3 \) digits replacements.
- Using 1, it is possible to generate the replacements more efficiently by adding to the current number the mask multiplied by the nth digit. For example, if the current number is \( 12345 \) and the mask is \( 00101 \), then the replacement is \( 12345 + 101 * d \).
Using these observations, it is possible to compute much more efficiently the prime digit replacements.
From solution2.py:
def is_nth_prime_value_family(n):
for d in range(3): # Observation 2
mask = 0
occurrences = 0
for i, m in enumerate(str(n)[::-1]): # Reverse string for easier mask creation
if m == str(d):
mask += 10**i
occurrences += 1
if occurrences == 0 or occurrences % 3 != 0: # Observation 3
continue
seq_len = 0
for r in range(10 - d):
if seq_len + 10 - r < 8: # Observation 2
break
if isprime(n + r * mask): # Observation 4
seq_len += 1
if seq_len == 8:
return n
The remaining step is the same as the Brute force approach.
From solution2.py:
def prime_digit_replacements():
for i in sieve:
res = is_nth_prime_value_family(i)
if res is not None:
return res
Solution
121313
Permuted multiples
It can be seen that the number, \( 125874 \), and its double, \( 251748 \), contain exactly the same digits, but in a different order.
Find the smallest positive integer, x, such that \( 2 \)x, \( 3 \)x, \( 4 \)x, \( 5 \)x, and \( 6 \)x, contain the same digits.
Brute force
The brute force approach for this problem is very simple, as the task of identifying numbers sharing the same digit has already been solved in the Prime permutations problem with the Brute force approach.
The remaining step consist of iterating through all positive numbers until all products wth number from 2 to 6 are permutations of the original integer.
From solution1.py:
def permuted_multiples():
for i in itertools.count(1):
if all(sorted(str(i)) == sorted(str(i * j)) for j in range(2, 7)):
return i
Observation is insight
Although the Brute force approach can effectively solve the problem, exploring alternative methodologies can offer valuable insights. In this case, several pertinent observations can be made:
- The number must be a multiple of \( 9 \), because every number are congruent to the sum of their digits modulo \( 9 \), thus \( x \equiv s \pmod{9} \), where \( s \) is the sum of digits of \( x \). Since \( 2x \equiv s \pmod{9} \), it follows that \( 2x - x \equiv s - s \pmod{9} \), which implies that \( x \equiv 0 \pmod{9} \).
- The first digit of the number must be \( 1 \), otherwise \( 2x \) would have one more digit than \( x \).
- According to the previous observation, \( 2x \) must start with \( 2 \) or \( 3 \), \( 3x \) must start with \( 3 \) or \( 4 \) and so on. Therefore, the number must at least contain 6 digits to satisfy to contain digits from \( 1 \) to \( 6 \).
- The number must contain a \( 0 \) or a \( 5 \) because \( 5x \) is obviously a multiple of \( 5 \).
It's actually possible to continue with the observation and find the solution by hand.
From solution2.py:
def permuted_multiples():
for i in itertools.count(100008, 9): # Observation 1 and 4
s = str(i)
if int(s[0]) != 1 or all(d not in s for d in "05"): # Observation 2 and 3
continue
if all(sorted(s) == sorted(str(i * j)) for j in range(2, 7)):
return i
It is worth noting that the solution is trivial if one know the property of \frac{1}{7} in decimal representation.
Solution
142857
Combinatoric selections
There are exactly ten ways of selecting three from five, \( 12345 \):
\[ 123, 124, 125, 134, 135, 145, 234, 235, 245,\text{ and }345 \]
In combinatorics, we use the notation, \( \displaystyle \binom 5 3 = 10 \).
In general, \( \displaystyle \binom n r = \dfrac{n!}{r!(n-r)!} \), where \( r \le n \), \( n!=n \times (n-1) \times ... \times 3 \times 2 \times 1 \), and \( 0!=1 \).
It is not until n \( =23 \), that a value exceeds one-million: \( \displaystyle \binom{23}{10}=1144066 \).
How many, not necessarily distinct, values of \( \displaystyle \binom n r \) for \( 1 \le n \le 100 \), are greater than one-million?
Brute force
A direct approach to determine all distinct values of \( \displaystyle \binom n r \leq 1000000 \) for \( 1 \le n \le 100 \) is as follows:
- Calculate \( \displaystyle \binom n r \) using the formula \( \displaystyle \binom n r = \dfrac{n!}{r!(n-r)!} \).
- Iterate over each \( n \) from \( 1 \) to \( 100 \) and \( r \) from \( 1 \) to \( n \) and count the number of \( \displaystyle \binom n r > 1,000,000 \).
The first task can be simply implemented using the math.factorial function.
From solution1.py:
def ncr(n, r):
return int((factorial(n) / (factorial(r) * factorial(n - r))))
The solution is then simpy implemented by iterating over all \( n \) and \( r \) and counting the number of \( \displaystyle \binom n r \) that are greater than \( 1,000,000 \).
From solution1.py:
def combinatoric_selections():
return sum(ncr(n, r) > 1000000 for n in range(23, 101) for r in range(1, n))
Pascal's Triangle
Pascal's triangle is a triangular array of the binomial coefficients. A small example of the Pascal's triangle is depicted below:
\[ \begin{align} &1\\ &1\ 1\\ &1\ 2\ \ 1\\ &1\ 3\ \ 3\ \ 1\\ &1\ 4\ \ 6\ \ 4\ \ 1\\ &1\ 5\ 10\ 10\ 5\ 1\\ \end{align} \]
The rows of the triangle are indexed from \( 1 \) to \( n \) and the columns are indexed from \( 1 \) to \( r \).
It describes the symmetry of the binomial coefficients, which is the reason why it is only necessary to calculate half of the triangle. Furthermore, if a coefficient is larger than \( n \), all coefficients between it and its mirror on the same row will also be larger than \( n \). This observation allows for more efficient iteration over the triangle. (1)
Furthermore, recomputing the binomial coefficients is very inefficient, which is why using a cache table for the factorials is a good idea. Alternatively, the binomial coefficients can be computed using the previous row by applying the following formula: \[ \binom{n}{r} = \binom{n - 1}{r - 1} + \binom{n - 1}{r} \]
The downside of this approach is that all the coefficients of the previous row have to be computed, which is unnecessary as stated in the first observation. Therefore, the following formula is used to compute the coefficients, which only requires information about the current row: (2) \[ \binom{n}{1} = n\\ \binom{n}{r} = \dfrac{n - r + 1}{r} \binom{n}{r - 1} \]
From solution2.py:
def combinatoric_selections():
res = 0
for n in range(23, 101):
ncr = n
for r in range(2, n // 2 + 1):
ncr = (ncr * (n - r + 1)) // r # Observation 2
if ncr > 1000000:
res += n - 2 * r + 1 # Observation 1
break
return res
Solution
4075
Poker hands
In the card game poker, a hand consists of five cards and are ranked, from lowest to highest, in the following way:
- High Card: Highest value card.
- One Pair: Two cards of the same value.
- Two Pairs: Two different pairs.
- Three of a Kind: Three cards of the same value.
- Straight: All cards are consecutive values.
- Flush: All cards of the same suit.
- Full House: Three of a kind and a pair.
- Four of a Kind: Four cards of the same value.
- Straight Flush: All cards are consecutive values of same suit.
- Royal Flush: Ten, Jack, Queen, King, Ace, in same suit.
The cards are valued in the order: \( 2 \), \( 3 \), \( 4 \), \( 5 \), \( 6 \), \( 7 \), \( 8 \), \( 9 \), \( 10 \), Jack, Queen, King, Ace.
If two players have the same ranked hands then the rank made up of the highest value wins; for example, a pair of eights beats a pair of fives (see example \( 1 \) below). But if two ranks tie, for example, both players have a pair of queens, then highest cards in each hand are compared (see example \( 4 \) below); if the highest cards tie then the next highest cards are compared, and so on.
Consider the following five hands dealt to two players:
Hand Player 1 Player 2 Winner 1 5H 5C 6S 7S KD Pair of Fives2C 3S 8S 8D TD Pair of EightsPlayer 2 2 5D 8C 9S JS AC Highest card Ace2C 5C 7D 8S QH Highest card QueenPlayer 1 3 2D 9C AS AH AC Three Aces3D 6D 7D TD QD Flush with DiamondsPlayer 2 4 4D 6S 9H QH QC Pair of Queens
Highest card Nine3D 6D 7H QD QS Pair of Queens
Highest card SevenPlayer 1 5 2H 2D 4C 4D 4S Full House
With Three Fours3C 3D 3S 9S 9D Full House
with Three ThreesPlayer 1 The file, poker.txt, contains one-thousand random hands dealt to two players. Each line of the file contains ten cards (separated by a single space): the first five are Player \( 1 \)'s cards and the last five are Player \( 2 \)'s cards. You can assume that all hands are valid (no invalid characters or repeated cards), each player's hand is in no specific order, and in each hand there is a clear winner.
How many hands does Player \( 1 \) win?
Brute force
For once, this problem only requires implementation of poker rules and does not involve any mathematical or algorithmic concepts. While the rules are straightforward, it can be tedious to implement due to the many possible outcomes. It is important to understand how to compare two hands to write less verbose code and not avoid missing some outcomes.
The rules for comparing hands are as follows:
- The hand with the highest rank wins.
- If two hands have the same rank, the one with the highest card wins.
- If two hands have the same rank and the same highest card, the one with the second-highest card wins and so on.
There is a special case for the Full House rank, for example, the Full House 4D 4S 4H 2C 2D is better than the Full House 3D 3S 3H 5C 5D because the three fours are better than the three threes (even if the pair of fives is better than the pair of twos).
Therefore, the rank of the hand alone is not sufficient to compare two hands, it is also required to know the occurrences of each card rank.
There may be more tricky cases (depending on the poker variant), but this is enough to solve the problem.
The input file is read using read_file function which returns a simple list of all cards of both hands.
From read_file.py:
def read_file(filename):
with open(filename, "r") as file:
return [line.split() for line in file.read().splitlines()]
For convenience and readability, Rank, Suit and Hand enums are defined and the from_string function is used to parse the input strings into cards.
Then, three information are extracted from each hand:
- The list of cards (sorted by occurrence and rank).
- If the hand is straight (all cards have consecutive ranks).
- If the hand is flush (all cards have the same suit).
Creating a tuple with rank of the hand and the list of cards (sorted by occurrence and rank) is enough to compare two hands.
From solution1.py:
def get_hand(hand):
values = sorted([Card.from_string(card[0]) for card in hand])
occ, values = zip(*sorted(((v, k) for k, v in Counter(values).items()), reverse=True))
is_straight = all(values[i].value == values[i + 1].value + 1 for i in range(len(values) - 1))
is_flush = len(set(card[1] for card in hand)) == 1
if occ == (4, 1):
hand = Hand.FOUR_OF_A_KIND
elif occ == (3, 2):
hand = Hand.FULL_HOUSE
elif occ == (3, 1, 1):
hand = Hand.THREE_OF_A_KIND
elif occ == (2, 2, 1):
hand = Hand.TWO_PAIR
elif occ == (2, 1, 1, 1):
hand = Hand.ONE_PAIR
elif is_straight and is_flush and values[0] == Card.ACE:
hand = Hand.ROYAL_FLUSH
elif is_straight and is_flush:
hand = Hand.STRAIGHT_FLUSH
elif is_flush:
hand = Hand.FLUSH
elif is_straight:
hand = Hand.STRAIGHT
elif occ == (1, 1, 1, 1, 1):
hand = Hand.HIGH_CARD
else:
raise ValueError("Invalid hand")
return hand, *values
The rest is just a matter of iterating over all the hands and counting the number of wins for player 1.
From solution1.py:
def poker_hands(file):
return sum(get_hand(hand[:5]) > get_hand(hand[5:]) for hand in read_file(file))
Solution
376
Lychrel numbers
If we take \( 47 \), reverse and add, \( 47+74=121 \), which is palindromic.
Not all numbers produce palindromes so quickly. For example,
\[ 349 + 943 = 1292,\\\\ 1292 + 2921 = 4213\\\\ 4213 + 3124 = 7337 \]
That is, \( 349 \) took three iterations to arrive at a palindrome.
Although no one has proved it yet, it is thought that some numbers, like \( 196 \), never produce a palindrome. A number that never forms a palindrome through the reverse and add process is called a Lychrel number. Due to the theoretical nature of these numbers, and for the purpose of this problem, we shall assume that a number is Lychrel until proven otherwise. In addition you are given that for every number below ten-thousand, it will either (i) become a palindrome in less than fifty iterations, or, (ii) no one, with all the computing power that exists, has managed so far to map it to a palindrome. In fact, \( 10677 \) is the first number to be shown to require over fifty iterations before producing a palindrome: \( 4668731596684224866951378664 \) (\( 53 \) iterations, \( 28 \)-digits).
Surprisingly, there are palindromic numbers that are themselves Lychrel numbers; the first example is \( 4994 \).
How many Lychrel numbers are there below ten-thousand?
NOTE: Wording was modified slightly on \( 24 \) April \( 2007 \) to emphasise the theoretical nature of Lychrel numbers.
Brute force
The problem requires to find the number of Lychrel numbers below 10,000. A Lychrel number is a natural number that cannot become a palindrome through the process of iteratively reversing the number and adding it to the original number. In this problem, a number is considered a Lychrel number if fails to form a palindrome within 1 to 50 iterations.
The first step is to write a function that checks if a number is a Lychrel number.
From solution1.py:
def is_lychrel(n):
for _ in range(50):
n += int(str(n)[::-1])
if str(n) == str(n)[::-1]:
return False
return True
Then, iterating through all numbers below 10000 and checking is enough to solve the problem.
From solution1.py:
def lychrel_numbers():
return sum(is_lychrel(n) for n in range(1, 10000))
Solution
249
Powerful digit sum
A googol (\( 10100 \)) is a massive number: one followed by one-hundred zeros; \( 100100 \) is almost unimaginably large: one followed by two-hundred zeros. Despite their size, the sum of the digits in each number is only \( 1 \).
Considering natural numbers of the form, ab, where a, b \( <100 \), what is the maximum digital sum?
Brute force
Computing the sum of digits of a number is a task that we already know.
From solution1.py:
def digits_sum(n):
return sum(map(int, str(n)))
Then, we can solve the problem by iterating over all the possible values of a and b, and keeping track of the maximum sum.
From solution1.py:
def powerful_digit_sum():
return max(digits_sum(a**b) for a in range(1, 100) for b in range(1, 100))
Solution
972
Square root convergents
It is possible to show that the square root of two can be expressed as an infinite continued fraction.
\[ \sqrt 2 =1+ \frac 1 {2+ \frac 1 {2 +\frac 1 {2+ \dots}}} \]
By expanding this for the first four iterations, we get:
\( 1 + \frac 1 2 = \frac 3 2 = 1.5 \)
\( 1 + \frac 1 {2 + \frac 1 2} = \frac 7 5 = 1.4 \)
\( 1 + \frac 1 {2 + \frac 1 {2+\frac 1 2}} = \frac {17}{12} = 1.41666 \dots \)
\( 1 + \frac 1 {2 + \frac 1 {2+\frac 1 {2+\frac 1 2}}} = \frac {41}{29} = 1.41379 \dots \)
The next three expansions are \( \frac{99}{70} \), \( \frac{239}{169} \), and \( \frac{577}{408} \), but the eighth expansion, \( \frac{1393}{985} \), is the first example where the number of digits in the numerator exceeds the number of digits in the denominator.
In the first one-thousand expansions, how many fractions contain a numerator with more digits than the denominator?
Brute force
This problem involves manipulating numerators and denominators of fractions, and understing the recurrence relation between them at each step is the key to solving it.
For example, starting with \( 1 + \color{red}{\frac{1}{2}} = \frac{3}{2} \), when computing \( 1 + \frac{1}{2 + \color{red}{\frac{1}{2}}} = \frac{5}{2} \), we notice that the denominator is always \( 2 \) plus the fraction of the previous equation.
To compute the new numerator and denominator, the first step is to add \( 2 \) to the fraction, which is equivalent to adding \( 2 \times \text{denominator} \) to the numerator. The second step is to apply the inverse of the fraction, which simply means swapping the numerator and denominator.
From solution1.py:
def new_fraction(numerator, denominator):
return denominator, 2 * denominator + numerator
The last step is to add one to this fraction, which is equivalent of adding the denominator to the numerator. If the new numerator has more digits than the denominator, increment the counter.
From solution1.py:
def square_root_convergents():
numerator = 0
denominator = 1
count = 0
for _ in range(1000):
numerator, denominator = new_fraction(numerator, denominator)
if len(str(numerator + denominator)) > len(str(denominator)):
count += 1
return count
A better recurrence?
With a bit of algebra, we can explain the recurrence relation in a more elegant way:
\[ \begin{align} x_n &= 1 + \frac{a_n}{b_n}\\ x_{n+1} &= 1 + \frac{1}{2 + \frac{a_n}{b_n}}\\ \end{align} \]
It should be clear than \( 2 + \frac{a_n}{b_n} = 1 + x_n \), so we can rewrite the second equation as:
\[ \begin{align} x_{n+1} &= 1 + \frac{1}{1 + x_n}\\ x_{n+1} &= \frac{2 + x_n}{1 + x_n}\\ \end{align} \]
We are not actually interested in \( x_{n} \), but in the numerator and denominator of \( x_{n} \), thus if we have \(x_n = \frac{p_n}{q_n}\), we can rewrite the last equation as:
\[ x_{n+1} = \frac{p_{n+1}}{q_{n+1}} = \frac{2 + \frac{p_n}{q_n}}{1 + \frac{p_n}{q_n}} = \frac{\frac{2q_n + p_n}{q_n}}{\frac{q_n + p_n}{q_n}} = \frac{2q_n + p_n}{q_n + p_n}\\ \]
This recurrence is better than the one used in the previous solution, because it explicitly gives the numerator and denominator of \( x_{n} \).
From solution2.py:
def square_root_convergents():
pn = 1
qn = 1
count = 0
for _ in range(1000):
pn, qn = 2 * qn + pn, qn + pn
if len(str(pn)) > len(str(qn)):
count += 1
return count
Solution
153
Spiral primes
Starting with \( 1 \) and spiralling anticlockwise in the following way, a square spiral with side length \( 7 \) is formed.
\[ \color{red}{37}\ 36\ 35\ 34\ 33\ 32\ \color{red}{31}\\\\ 38\ \color{red}{17}\ 16\ 15\ 14\ \color{red}{13}\ 30\\\\ 39\ 18\ \ \color{red}{5}\ \ \ 4\ \ \ \color{red}{3}\ \ 12\ 29\\\\ 40\ 19\ \ 6\ \ \ 1\ \ \ 2\ \ 11\ 28\\\\ 41\ 20\ \ \color{red}{7}\ \ \ 8\ \ \ 9\ \ 10\ 27\\\\ 42\ 21\ 22\ 23\ 24\ 25\ 26\\\\ \color{red}{43}\ 44\ 45\ 46\ 47\ 48\ 49 \]
It is interesting to note that the odd squares lie along the bottom right diagonal, but what is more interesting is that \( 8 \) out of the \( 13 \) numbers lying along both diagonals are prime; that is, a ratio of \( \frac{8}{13} \approx 62% \).
If one complete new layer is wrapped around the spiral above, a square spiral with side length \( 9 \) will be formed. If this process is continued, what is the side length of the square spiral for which the ratio of primes along both diagonals first falls below \( 10 \)%?
Brute force
This problem should reminisce you of Problem 28. Utilizing information from the previous problem, the solution becomes straightforward and involves iterating through each value in the corner until the ratio of primes falls below 10%.
From solution1.py:
def spiral_primes():
res = 0
for i in itertools.count(3, 2):
res += (
isprime(i**2) + isprime(i**2 - (i - 1)) + isprime(i**2 - 2 * (i - 1)) + isprime(i**2 - 3 * (i - 1))
)
if res < (2 * i - 1) / 10:
return i
Solution
26241
XOR decryption
Each character on a computer is assigned a unique code and the preferred standard is ASCII (American Standard Code for Information Interchange). For example, uppercase A \( =65 \), asterisk (\( * \)) \( =42 \), and lowercase k \( =107 \).
A modern encryption method is to take a text file, convert the bytes to ASCII, then XOR each byte with a given value, taken from a secret key. The advantage with the XOR function is that using the same encryption key on the cipher text, restores the plain text; for example, \( 65 \) XOR \( 42=107 \), then \( 107 \) XOR \( 42=65 \).
For unbreakable encryption, the key is the same length as the plain text message, and the key is made up of random bytes. The user would keep the encrypted message and the encryption key in different locations, and without both "halves", it is impossible to decrypt the message.
Unfortunately, this method is impractical for most users, so the modified method is to use a password as a key. If the password is shorter than the message, which is likely, the key is repeated cyclically throughout the message. The balance for this method is using a sufficiently long password key for security, but short enough to be memorable.
Your task has been made easy, as the encryption key consists of three lower case characters. Using p059_cipher.txt (right click and 'Save Link\( / \)Target As\( ... \)'), a file containing the encrypted ASCII codes, and the knowledge that the plain text must contain common English words, decrypt the message and find the sum of the ASCII values in the original text.
Brute force
Decrypting ciphertexts is a common task in cryptography. This problem provides a ciphertext and the key length. Given the short length of the key, one solution is to try all possible keys and see which one gives a plaintext that makes sense. However, since I'm too lazy to check all the outputs, let's think about it a bit more.
Frequency analysis is a method used to break simple substitution ciphers. Counting the number of occurrences of each character in the ciphertext and comparing it with the frequencies of the letters in the English language can give some clues about the plaintext. As 'e' is the most common letter in English, the most common letter in the ciphertext is likely to be 'e'.
To find the key, the first step is to split the ciphertext into blocks of length equal to the key length. Then, applying XOR to the most common character in each block with 'e' should give each block's key.
The first step is to parse the ciphertext and get a list of integers to apply XOR to.
From solution1.py:
def parse_file():
with open("cipher.txt", "r") as f:
return [int(x) for x in f.read().split(",")]
Using collections.Counter.most_common to determine the most common character in each block and itertools.cycle to iterate over the key repeatedly will be helpful. Lastly, applying XOR operations between each character in the ciphertext and the corresponding character of the key gives the plaintext.
Due to the nature of the text, the most frequent character is more likely to be ' ' (space) than 'e'. This is because the ciphertext is an English text, as a result, applying XOR using ' ' to the most common character in each block yields the correct solution.
From solution1.py:
def xor_decryption():
code = parse_file()
k1 = Counter(code[::3]).most_common(1)[0][0] ^ ord(" ")
k2 = Counter(code[1::3]).most_common(1)[0][0] ^ ord(" ")
k3 = Counter(code[2::3]).most_common(1)[0][0] ^ ord(" ")
key = [k1, k2, k3]
res = [chr(c ^ p) for (c, p) in zip(parse_file(), itertools.cycle(key))]
return sum(ord(c) for c in res)
Solution
129448
Prime pair sets
The primes \( 3 \), \( 7 \), \( 109 \), and \( 673 \), are quite remarkable. By taking any two primes and concatenating them in any order the result will always be prime. For example, taking \( 7 \) and \( 109 \), both \( 7109 \) and \( 1097 \) are prime. The sum of these four primes, \( 792 \), represents the lowest sum for a set of four primes with this property.
Find the lowest sum for a set of five primes for which any two primes concatenate to produce another prime.
Brute force
The problem requires finding the set of five primes that has the lowest sum and for which any two primes concatenate to produce another prime. A brute force approach can be used, but it requires to generate all the primes up to a certain arbitrary limit. Then, 5 nested loops are used to find the first set of five primes that satisfy the condition. If the concatenation of two primes is not prime, the search for the current set of primes can be stopped.
Determining whether two concatenated primes are prime is done by converting the numbers to strings and checking whether the concatenation of the strings is prime. It is worth noting that another method involving logarithms can be used to determine whether the concatenation of two numbers is prime, but it is not as straightforward as the string approach.
From solution1.py:
def concat(p1, p2):
return isprime(int(str(p1) + str(p2))) and isprime(int(str(p2) + str(p1)))
The rest is the 5 nested loops, for each loop, only the new prime is checked against the previous ones. The limit is set to 10000, which is enough to find the solution.
From solution1.py:
def prime_pair_sets():
primes = list(sieve.primerange(10000))
for i, p1 in enumerate(primes):
for j, p2 in enumerate(primes[:i]):
if any(not concat(p, p2) for p in (p1,)):
continue
for k, p3 in enumerate(primes[:j]):
if any(not concat(p, p3) for p in (p1, p2)):
continue
for l, p4 in enumerate(primes[:k]):
if any(not concat(p, p4) for p in (p1, p2, p3)):
continue
for p5 in primes[:l]:
if all(concat(p, p5) for p in (p1, p2, p3, p4)):
return p1 + p2 + p3 + p4 + p5
This solution may not yield the smallest sum because the order of iteration is not designed to minimize the sum.
Clique's graph theory
Another solution is to use the clique graph theory. A clique is a subset of vertices in an undirected graph, such that every two distinct vertices in the clique are adjacent. In this problem, a graph can be defined with vertices representing primes and edges representing the concatenation of two primes being prime. The solution can be found by finding the clique of size 5 with the smallest sum. Indeed, a clique of size 5 is a set of 5 vertices (primes) such that every two vertices are adjacent (every concatenation of two primes is prime).
To simplify the process of creating the graph and finding the clique, the networkx library is used.
From solution2.py:
def prime_pair_sets():
primes = list(sieve.primerange(10000))
pairs = ((p1, p2) for p1 in primes for p2 in primes if p1 < p2 and concat(p1, p2))
graph = nx.Graph()
graph.add_edges_from(pairs)
five_cliques = [sum(clique) for clique in find_cliques(graph) if len(clique) == 5]
return sorted(five_cliques)[0]
Solution
26033
Cyclical figurate numbers
Triangle, square, pentagonal, hexagonal, heptagonal, and octagonal numbers are all figurate (polygonal) numbers and are generated by the following formulae:
\[ \begin{align} & Triangle && P_{3,n} = n(n+1)/2 && 1, 3, 6, 10, 15, ... \\ & Square && P_{4,n} = n^2 && 1, 4, 9, 16, 25, ... \\ & Pentagonal && P_{5,n} = n(3n-1)/2 && 1, 5, 12, 22, 35, ... \\ & Hexagonal && P_{6,n} = n(2n-1) && 1, 6, 15, 28, 45, ... \\ & Heptagonal && P_{7,n} = n(5n-3)/2 && 1, 7, 18, 34, 55, ... \\ & Octagonal && P_{8,n} = n(3n-2) && 1, 8, 21, 40, 65, ... \end{align} \]
The ordered set of three \( 4 \)-digit numbers: \( 8128 \), \( 2882 \), \( 8281 \), has three interesting properties.
- The set is cyclic, in that the last two digits of each number is the first two digits of the next number (including the last number with the first).
- Each polygonal type: triangle \( (P_{3,127}=8128) \), square \( (P_{4,91}=8281) \), and pentagonal \( (P_{5,44}=2882) \), is represented by a different number in the set.
- This is the only set of \( 4 \)-digit numbers with this property.
Find the sum of the only ordered set of six cyclic \( 4 \)-digit numbers for which each polygonal type: triangle, square, pentagonal, hexagonal, heptagonal, and octagonal, is represented by a different number in the set.
Brute force
The problem is to find the sum of the set of six cyclic 4-digit numbers for which each polygonal type is represented by a cyclic number in the set. To resume, this problem has 3 constraints:
- The numbers are 4-digit numbers.
- The numbers are cyclic.
- Each number is a polygon of a given type.
The brute force solution for this problem, while simple, is not easy to implement due to its recursive nature.
The idea is to try every 4-digit number until a polygon is found. Starting with the last two digits of the previous polygon, this operation should be repeated 5 times. If all polygon types have been found, and the last two digits of the last polygon are the same as the first two digits of the first polygon, the solution is the sum of this cycle.
Overall, the recursive algorithm requires to keep track of the remaining polygon types, the current number, and the current cycle. The remaining polygon types is represented with a list of functions that return whether a number is a polygon.
From solution1.py:
def find_cycle(first_two_digits, is_polygonals, cycle):
if not is_polygonals:
if cycle[0] // 100 == cycle[-1] % 100:
return cycle
return []
for last_two_digits in range(10, 100):
p = first_two_digits * 100 + last_two_digits
for i, is_polygonal in enumerate(is_polygonals):
if is_polygonal(p):
new_cycle = find_cycle(last_two_digits, is_polygonals[:i] + is_polygonals[i + 1 :], cycle + [p])
if new_cycle:
return new_cycle
return []
The rest is to actually build the list of polygon types and to call the recursive function. The formulas for each polygon type are similar to the one in Problem 0042, and can be found in the source code. Therefore, they will not be repeated in this text for brevity.
From solution1.py:
def cyclical_figurate_numbers():
is_triangular = lambda n: ((1 + (1 + 8 * n) ** 0.5) / 2).is_integer()
is_square = lambda n: (n**0.5).is_integer()
is_pentagonal = lambda n: ((1 + (1 + 24 * n) ** 0.5) / 6).is_integer()
is_hexagonal = lambda n: ((1 + (1 + 8 * n) ** 0.5) / 4).is_integer()
is_heptagonal = lambda n: ((3 + (9 + 40 * n) ** 0.5) / 10).is_integer()
is_octagonal = lambda n: ((1 + (1 + 3 * n) ** 0.5) / 3).is_integer()
is_polygonals = [is_triangular, is_square, is_pentagonal, is_hexagonal, is_heptagonal, is_octagonal]
for i in range(10, 100):
cycle = find_cycle(i, is_polygonals, [])
if cycle:
return sum(cycle)
return []
Caching polygonal numbers
Instead of iterating through all 4-digit numbers, pre-computing all polygonal numbers and then iterating through them is a better approach.
It does not change the find_cycle function by much, instead of trying every 4-digit number, it tries every polygonal number.
From solution2.py:
def find_cycle(first_two_digits, polygonals, cycle):
if not polygonals:
if cycle[0] // 100 == cycle[-1] % 100:
return cycle
return []
for i in range(len(polygonals)):
for p in polygonals[i]:
if p // 100 == first_two_digits:
new_cycle = find_cycle(p % 100, polygonals[:i] + polygonals[i + 1 :], cycle + [p])
if new_cycle:
return new_cycle
return []
The rest is also very similar, the difference is the list of polygon types which is now a list of sets of polygonal numbers and the iteration is done starting with the octogonals numbers.
From solution2.py:
def cyclical_figurate_numbers():
triangles = set(n * (n + 1) // 2 for n in range(45, 141))
squares = set(n**2 for n in range(32, 100))
pentagonals = set(n * (3 * n - 1) // 2 for n in range(26, 82))
hexagonals = set(n * (2 * n - 1) for n in range(23, 71))
heptagonals = set(n * (5 * n - 3) // 2 for n in range(21, 64))
octagonals = set(n * (3 * n - 2) for n in range(19, 59))
polygonals = [triangles, squares, pentagonals, hexagonals, heptagonals]
for p in octagonals:
cycle = find_cycle(p, polygonals, [p])
if cycle:
return sum(cycle)
return []
Solution
28684
Cubic permutations
The cube, \( 41063625 \) (\( 345^3 \)), can be permuted to produce two other cubes: \( 56623104 \) (\( 384^3 \)) and \( 66430125 \) (\( 405^3 \)). In fact, \( 41063625 \) is the smallest cube which has exactly three permutations of its digits which are also cube.
Find the smallest cube for which exactly five permutations of its digits are cube.
Brute force
The problem is to find the smallest cube \( n^3 \) such that it has at least \( 5 \) permutations that are also cubes. The brute force approach is exactly what it sounds like:
- Generate all cubes \( n^3 \).
- Generate all permutations of this cube .
- Check if the permutations are cubes with the same number of digits and is not already counted.
- If there are \( 5 \) or more permutations that meet the criteria, then the solution is found
Using itertools.permutations greatly simplifies the second step.
From solution1.py:
def cubic_permutations():
for cube in (i**3 for i in itertools.count(1)): # Condition 1
cubes = {cube}
for p in itertools.permutations(str(cube)): # Condition 2
new_cube = int("".join(p))
if p[0] != "0" and is_cube(new_cube) and new_cube not in cubes: # Condition 3
cubes.add(new_cube)
if len(cubes) >= 5: # Condition 4
return min(cubes)
Although this method works for the given example, it is too slow to solve the problem.
Iterating and caching
The main issue with the Brute force approach is that it checks the same permutations multiples times and many of them are not cubes, making it very inefficient.
To overcome this issue, we can use a similar approach to Problem 0049 which involves:
- Generating all cubes \( n^3 \).
- Grouping the cubes with the same permutation together.
- If one of the groups has at least \( 5 \) cubes, the solution is found.
From solution2.py:
def cubic_permutations():
permutations = defaultdict(list)
for cube in (i**3 for i in itertools.count(1)): # Condition 1
ordered_digits = "".join(sorted(str(cube)))
permutations[ordered_digits].append(cube) # Condition 2
if len(permutations[ordered_digits]) >= 5: # Condition 3
return min(permutations[ordered_digits])
Note that the function actually returns the smallest cube of the first group with at least \( 5 \) cubes. While this is sufficient for this problem, it will not necessarily provide the correct answer with groups of bigger sizes, like \( 6 \).
Solution
127035954683
Powerful digit counts
The \( 5 \)-digit number, \( 16807=7^5 \), is also a fifth power. Similarly, the \( 9 \)-digit number, \( 134217728=8^9 \), is a ninth power.
How many n-digit positive integers exist which are also an nth power?
Brute force
The problem is to determine the number of positive integers that are nth power. Here, positive integers refer to integers greater than 0.
The brute force algorithm for solving this problem is relatively straightforward:
- Iterate through all positive integers.
- For each integer, iterate through all positive powers.
- If the length of the computer number is equal to the power, increment the counter.
However, the challenge lies in determining when to terminate both iterations.
To express the problem mathematically, we search all \( n \) and \( x \) such that \( 10^{n-1} \leq x^n < 10^n \). It follows that \( x \) must be less than \( 10 \), and \( 10^{n-1} \) grows faster than \( x^n \) since \( x < 10 \). Therefore, the iteration over \( n \) can be stopped when \( 10^{n-1} > x^n \).
From solution1.py:
def powerful_digit_counts():
res = 0
for i in range(1, 10):
for j in itertools.count(1):
if len(str(i**j)) == j:
res += 1
elif len(str(i**j)) < j:
break
return res
Back to initial equation
In the Brute force solution, we found that \( 1 < x < 10 \) and \( 10^{n-1} > x^n \) for \( n \) sufficiently large. Rather than iterating through all \( n \) until \( 10^{n-1} > x^n \), solving the equation \( 10^{n-1} = x^n \) for \( n \) gives the exact limit for \( n \).
\[ \begin{align} &\Leftrightarrow 10^{n-1} = x^n \\ &\Leftrightarrow \log_{10}\left(10^{n-1}\right) = \log_{10}\left(x^n\right) \\ &\Leftrightarrow n - 1 = n\log_{10}\left(x\right) \\ &\Leftrightarrow n(1 - \log_{10}\left(x\right)) = 1 \\ &\Leftrightarrow n = \frac{1}{1 - \log_{10}\left(x\right)} \\ \end{align} \]
Since \( n \) is an integer, the limit is the largest integer for which the inequality holds true.
From solution2.py:
def powerful_digit_counts():
return sum(floor(1 / (1 - log10(i))) for i in range(1, 10))
Solution
49
Odd period square roots
All square roots are periodic when written as continued fractions and can be written in the form:
\( \displaystyle \quad \quad \sqrt{N}=a_0+\frac 1 {a_1+\frac 1 {a_2+ \frac 1 {a3+ \dots}}} \)
For example, let us consider \( \sqrt{23} \):
\( \quad \quad \sqrt{23}=4+\sqrt{23}-4=4+\frac 1 {\frac 1 {\sqrt{23}-4}}=4+\frac 1 {1+\frac{\sqrt{23}-3}7} \)
If we continue we would get the following expansion:
\( \displaystyle \quad \quad \sqrt{23}=4+\frac 1 {1+\frac 1 {3+ \frac 1 {1+\frac 1 {8+ \dots}}}} \)
The process can be summarised as follows:
\[ \begin{align} &a_0=4, \frac 1 {\sqrt{23}-4}=\frac {\sqrt{23}+4} 7=1+\frac {\sqrt{23}-3} 7\\ &a_1=1, \frac 7 {\sqrt{23}-3}=\frac {7(\sqrt{23}+3)} {14}=3+\frac {\sqrt{23}-3} 2\\ &a_2=3, \frac 2 {\sqrt{23}-3}=\frac {2(\sqrt{23}+3)} {14}=1+\frac {\sqrt{23}-4} 7\\ &a_3=1, \frac 7 {\sqrt{23}-4}=\frac {7(\sqrt{23}+4)} 7=8+\sqrt{23}-4\\ &a_4=8, \frac 1 {\sqrt{23}-4}=\frac {\sqrt{23}+4} 7=1+\frac {\sqrt{23}-3} 7\\ &a_5=1, \frac 7 {\sqrt{23}-3}=\frac {7 (\sqrt{23}+3)} {14}=3+\frac {\sqrt{23}-3} 2\\ \\ &a_6=3, \frac 2 {\sqrt{23}-3}=\frac {2(\sqrt{23}+3)} {14}=1+\frac {\sqrt{23}-4} 7\\ &a_7=1, \frac 7 {\sqrt{23}-4}=\frac {7(\sqrt{23}+4)} {7}=8+\sqrt{23}-4\\ \end{align} \]
It can be seen that the sequence is repeating. For conciseness, we use the notation \( \sqrt{23}=[4;(1,3,1,8)] \), to indicate that the block \( (1,3,1,8) \) repeats indefinitely.
The first ten continued fraction representations of (irrational) square roots are:
\[ \begin{align} &\sqrt{2}=[1;(2)],\text{period=1}\\ &\sqrt{3}=[1;(1,2)],\text{period=2}\\ &\sqrt{5}=[2;(4)],\text{period=1}\\ &\sqrt{6}=[2;(2,4)],\text{period=2}\\ &\sqrt{7}=[2;(1,1,1,4)],\text{period=4}\\ &\sqrt{8}=[2;(1,4)],\text{period=2}\\ &\sqrt{10}=[3;(6)],\text{period=1}\\ &\sqrt{11}=[3;(3,6)],\text{period=2}\\ &\sqrt{12}=[3;(2,6)],\text{period=2}\\ &\sqrt{13}=[3;(1,1,1,1,6)],\text{period=5}\\ \end{align} \]
Exactly four continued fractions, for \( N \le 13 \), have an odd period.
How many continued fractions for \( N \le 10,000 \) have an odd period?
Brute force
The solution asks for the number of continued fractions with an odd period. A continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. 1
To solve the problem, the first step is to understand the iterative nature of the continued fractions.
The continued fraction is defined using \( a_0 = \left\lfloor \sqrt{N} \right\rfloor \) as: \[ \begin{align} \sqrt{N} &= a_0 + \sqrt{N} - a_0\\ &= a_0 + \frac{1}{\frac{1}{\sqrt{N} - a_0}} = a_0 + \frac{1}{\frac{\sqrt{N} + a_0}{N - a_0^2}} = a_0 + \frac{1}{a_1 + \frac{\sqrt{N} - b_1}{c_1}}\\ \end{align}\\ \text{where } c_1 = N - a_0^2; \quad a_1 = \left\lfloor \frac{\sqrt{N} + a_0}{c_1} \right\rfloor; \quad b_1 = -(a_0 - a_1c_1) \]
Repeating the process gives:
\[ \begin{align} a_1 + \frac{\sqrt{N} - b_1}{c_1} &= a_1 + \frac{1}{\frac{c_1}{\sqrt{N} - b_1}} = a_1 + \frac{1}{\frac{\sqrt{N} + b_1}{\frac{N - b_1^2}{c_1}}} = a_1 + \frac{1}{a_2 + \frac{\sqrt{N} - b_2}{c_2}}\\ \end{align}\\ \text{where } c_2 = \frac{N - b_1^2}{c_1}; \quad a_2 = \left\lfloor \frac{\sqrt{N} + b_1}{c_2} \right\rfloor; \quad b_2 = -(b_1 - a_2c_2) \]
The process can be continued, and the following pattern can be observed:
\[ \begin{align} c_{n+1} &= \frac{N - b_n^2}{c_n}\\ a_{n+1} &= \left\lfloor \frac{\sqrt{N} + b_n}{c_{n+1}} \right\rfloor\\ b_{n+1} &= -(b_n - a_{n+1}c_{n+1}) \end{align} \]
The first equation can be rewritten as \( a_0 + \sqrt{N} - a_0 = a_0 + \frac{\sqrt{N} - a_0}{1} = a_0 + \frac{\sqrt{N} - b_0}{c_0} \) which results in the same pattern as the second equation and provides the initialisation for the iterative process. The iteration can be stopped when \( b_n \) and \( c_n \) repeat, because the continued fraction will also repeat itself.
From solution1.py:
def period_square_roots(n):
a_0 = floor(sqrt(n))
if a_0 * a_0 == n:
return 0
bn = a_0
cn = 1
remainders = {}
for pos in itertools.count(1):
cn = (n - (bn * bn)) / cn
an = floor((sqrt(n) + bn) / cn)
bn = -(bn - (an * cn))
if (bn, cn) in remainders:
return pos - remainders[bn, cn]
remainders[bn, cn] = pos
The solution can be computed by trying all the numbers \( N \) below \( 10000 \) and counting the number of continued fractions with an odd period.
From solution1.py:
def odd_period_square_roots():
return sum(period_square_roots(n) % 2 for n in range(2, 10001))
Another property of continued fractions
Going back to the equation:
\[ \frac{\sqrt{N} - b_1}{c_1} = a_2 + \frac{\sqrt{N} - b_2}{c_2} \]
and
\[ \begin{align} c_{n+1} &= \frac{N - b_n^2}{c_n}\\ a_{n+1} &= \left\lfloor \frac{\sqrt{N} + b_n}{c_{n+1}} \right\rfloor\\ b_{n+1} &= -(b_n - a_{n+1}c_{n+1}) \end{align} \]
The following can be deduced:
- \( b_2 < \sqrt{N} \), because \( c_2 = \frac{N - b_1^2}{c_1} \) is positive.
- \( b_2 \leq a_0 \), because \( a_0 = \left\lfloor \sqrt{N} \right\rfloor \).
- \( b_2 = a_2c_2 - b_1 \leq a_0 \)
If \( a_2 = 2a_0 \), then \( b_2 = 2a_0c_2 - b_1 \leq a_0 \), because all terms are positive integers we have \( c_2 = 1 \) and \( b_1 = a_0 \). Which results with \( b_2 = -(b_1 - a_2c_2) = -(a_0 - 2a_0) = a_0 \) The first expression becomes \( \frac{\sqrt{N} - b_1}{c_1} = a_2 + \frac{\sqrt{N} - b_2}{c_2} = 2a_0 + \frac{\sqrt{N} - a_0}{1} \) This is similar to the first iteration of the algorithm, which means that the sequence will repeat when \( a_n = 2a_0 \). The formal proof can be found in the paper On continued fractions of the square root of prime numbers.
This property is much easier to implement than remembering every \( b_n \) and \( c_n \).
From solution2.py:
def period_square_roots(n):
a_0 = floor(sqrt(n))
if a_0 * a_0 == n:
return 0
bn = a_0
cn = 1
for pos in itertools.count(1):
cn = (n - (bn * bn)) / cn
an = floor((sqrt(n) + bn) / cn)
bn = -(bn - (an * cn))
if an == 2 * a_0:
return pos
From solution2.py:
def odd_period_square_roots():
return sum(period_square_roots(n) % 2 for n in range(2, 10001))
Solution
1322
Convergents of e
The square root of \( 2 \) can be written as an infinite continued fraction.
\( \sqrt{2} = 1 + \dfrac{1}{2 + \dfrac{1}{2 + \dfrac{1}{2 + \dfrac{1}{2 + ...}}}} \)
The infinite continued fraction can be written, \( \sqrt{2} = [1; (2)] \), \( (2) \) indicates that \( 2 \) repeats ad infinitum. In a similar way, \( \sqrt{23} = [4; (1, 3, 1, 8)] \).
It turns out that the sequence of partial values of continued fractions for square roots provide the best rational approximations. Let us consider the convergents for \( \sqrt{2} \).
\[ \begin{align} &1+ \dfrac{1}{2} = \dfrac{3}{2} \\ &1+ \dfrac{1}{2 + \dfrac{1}{2}} = \dfrac{7}{5}\\ &1+ \dfrac{1}{2 + \dfrac{1}{2 + \dfrac{1}{2}}} = \dfrac{17}{12}\\ &1+ \dfrac{1}{2 + \dfrac{1}{2 + \dfrac{1}{2 + \dfrac{1}{2}}}} = \dfrac{41}{29}\\ \end{align} \]
Hence the sequence of the first ten convergents for \( \sqrt{2} \) are:
\( 1, \dfrac{3}{2}, \dfrac{7}{5}, \dfrac{17}{12}, \dfrac{41}{29}, \dfrac{99}{70}, \dfrac{239}{169}, \dfrac{577}{408}, \dfrac{1393}{985}, \dfrac{3363}{2378}, ... \)
What is most surprising is that the important mathematical constant, \( e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, ... , 1, 2k, 1, ...] \).
The first ten terms in the sequence of convergents for \( e \) are:
\( 2, 3, \dfrac{8}{3}, \dfrac{11}{4}, \dfrac{19}{7}, \dfrac{87}{32}, \dfrac{106}{39}, \dfrac{193}{71}, \dfrac{1264}{465}, \dfrac{1457}{536}, ... \)
The sum of digits in the numerator of the \( 10 \)th convergent is \( 1+4+5+7=17 \).
Find the sum of digits in the numerator of the \( 100 \)th convergent of the continued fraction for \( e \).
Brute force
The problem is to find the sum of the digits in the numerator of the 100th convergent of the continued fraction for \( e \).
The key to solve the problem is to understand the pattern of the numerator for each iteration. By observing the relation between the numerator, denominator and the convergent, the recursive relation should become evident. Starting with numerators \( h_1 \) and \( h_2 \), and convergent \( a_1 \), the recursive relationship can be defined as follows: \( h_n = a_n h_{n-1} + h_{n-2} \). As the convergent pattern is already given, computing the numerator for the \( 100 \)th convergent is a matter of applying the recursive relation \( 100 \) times.
From solution1.py:
def convergents_of_e():
an = [2] + [1 if i % 3 != 2 else 2 * (i // 3 + 1) for i in range(1, 100)]
h1, h2 = 0, 1
for i in range(100):
h1, h2 = h2, h1 + an[i] * h2
return sum(int(c) for c in str(h2))
Solution
272
Diophantine equation
Consider quadratic Diophantine equations of the form:
\[ x^{2} – Dy^{2} = 1 \]
For example, when D\( = \)1\( 3 \), the minimal solution in \( x \) is \( 6492 - 13 \times 1802=1 \).
It can be assumed that there are no solutions in positive integers when \( D \) is square.
By finding minimal solutions in x for \( D = \{2, 3, 5, 6, 7\} \), we obtain the following:
\[ 3^{2} – 2×2^{2} = 1\\\\ 2^{2} – 3×1^{2} = 1\\\\ \color{red}{9}^{2} – 5×4^{2} = 1\\\\ 5^{2} – 6×2^{2} = 1\\\\ 8^{2} – 7×3^{2} = 1 \]
Hence, by considering minimal solutions in \( x \) for \( D \leq 7 \), the largest \( x \) is obtained when \( D = 5 \).
Find the value of \( D \leq 1000 \) in minimal solutions of \( x \) for which the largest value of \( x \) is obtained.
Brute force
The problem is to find the value of \( D \leq 1000 \) for which \( x \) is maximised in the equation \( x^2 - Dy^2 = 1 \).
Brute forcing the solution is easy, for each \( D \leq 1000 \) that is not a perfect square, and for each \( x > 1 \), if \( y = \sqrt{\frac{x^2 - 1}{D}} \) is an integer, then \( x^2 - Dy^2 = 1 \) is satisfied.
From solution1.py:
def diophantine_equation():
res = 0
for d in range(2, 1001):
if sqrt(d).is_integer():
continue
for x in itertools.count(2):
if (sqrt((x**2 - 1) / d)).is_integer():
res = max(res, x)
break
return res
However, the brute force approach is not effective and does not provide the solution for \( D = 61 \) as \( x \) becomes too large...
Solving Pell's equations
This diophantine equation is called Pell's equation, and it is possible to solve it using the continued fraction expansion of \( \sqrt{D} \).
This method involves finding the numerator and denominator of the \( i \)-th convergent of \( \sqrt{D} \) denoted by \( h_i \) and \( k_i \) respectively, where \( h_i^2 - D k_i^2 = 1 \) for some \( i \). Furthermore, the first \( i \) that satisfies this condition corresponds to the smallest \( x \) that satisfies the equation.
With Problem 0065, we know the recurrence relation for computing \( h_i \) and \( k_i \) is:
\[ h_i = a_i h_{i-1} + h_{i-2}\\ k_i = a_i k_{i-1} + k_{i-2} \]
where \( a_i \) is the \( i \)-th convergent of \( \sqrt{D} \).
The cycle of convergent of \( \sqrt{D} \) can be computed using the method Another property of continued fractions.
From solution2.py:
def get_convergent_cycle(n):
a_0 = floor(sqrt(n))
res = []
if a_0 * a_0 == n:
return []
bn = a_0
cn = 1
for _ in itertools.count(1):
cn = (n - (bn * bn)) / cn
an = floor((sqrt(n) + bn) / cn)
bn = -(bn - (an * cn))
res.append(an)
if an == 2 * a_0:
return res
Then, using the recurrence relation, we can compute \( h_i \) and \( k_i \) and find the first \( i \) that satisfies \( h_i^2 - D k_i^2 = 1 \) for each \( D \leq 1000 \).
From solution2.py:
def diophantine_equation():
x, res = 0, 0
for d in range(2, 1001):
an = get_convergent_cycle(d)
if not an:
continue
h1, h2, k1, k2 = 1, floor(sqrt(d)), 0, 1
for i in itertools.count(0):
h1, h2 = h2, h1 + an[i % len(an)] * h2
k1, k2 = k2, k1 + an[i % len(an)] * k2
if h2 * h2 - d * k2 * k2 == 1:
x, res = max((h2, d), (x, res))
break
return res
Solution
Maximum path sum II
By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is \( 23 \).
\[ \color{red}{3}\\\\ 2\ \color{red}{4}\ 6\\\\ 8\ 5\ \color{red}{9}\ 3 \]
That is, \( 3+7+4+9=23 \).
Find the maximum total from top to bottom in triangle.txt (right click and 'Save Link/Target As...'), a \( 15 \)K text file containing a triangle with one-hundred rows.
NOTE: This is a much more difficult version of Problem 18. It is not possible to try every route to solve this problem, as there are \( 2^{99} \) altogether! If you could check one trillion (\( 10^12 \)) routes every second it would take over twenty billion years to check them all. There is an efficient algorithm to solve it. ;o)
Dynamic programming
This problem is the same as Problem 0018, but with a larger triangle.
As we did in the Dynamic programming solution for Problem 0018, we can reduce the triangle by replacing each number with the sum of itself and the largest number below it.
From solution1.py:
def maximum_path_sum_II(filename):
triangle = read_file(filename)
for i in range(len(triangle) - 2, -1, -1):
for j in range(len(triangle[i])):
triangle[i][j] += max(triangle[i + 1][j], triangle[i + 1][j + 1])
return triangle[0][0]
Solution
7273
Magic 5-gon ring
Consider the following "magic" \( 3 \)-gon ring, filled with the numbers \( 1 \) to \( 6 \), and each line adding to nine.
Working clockwise, and starting from the group of three with the numerically lowest external node (\( 4 \),\( 3 \),\( 2 \) in this example), each solution can be described uniquely. For example, the above solution can be described by the set: \( 4 \),\( 3 \),\( 2 \); \( 6 \),\( 2 \),\( 1 \); \( 5 \),\( 1 \),\( 3 \).
It is possible to complete the ring with four different totals: \( 9 \), \( 10 \), \( 11 \), and \( 12 \). There are eight solutions in total.
Total Solution Set 9 4,2,3; 5,3,1; 6,1,2 9 4,3,2; 6,2,1; 5,1,3 10 2,3,5; 4,5,1; 6,1,3 10 2,5,3; 6,3,1; 4,1,5 11 1,4,6; 3,6,2; 5,2,4 11 1,6,4; 5,4,2; 3,2,6 12 1,5,6; 2,6,4; 3,4,5 12 1,6,5; 3,5,4; 2,4,6 By concatenating each group it is possible to form \( 9 \)-digit strings; the maximum string for a \( 3 \)-gon ring is \( 432621513 \).
Using the numbers \( 1 \) to \( 10 \), and depending on arrangements, it is possible to form \( 16 \)- and \( 17 \)-digit strings. What is the maximum 16-digit string for a "magic" \( 5 \)-gon ring?
Brute force
The problem is to find the maximum 16-digit string for a "magic" 5-gon ring. In this context, a "magic" gon ring is valid if all lines add up to the same number.
To solve this problem the brute force way, we need to:
1. Generate all possible rings.
There exists multiple possible representation of a ring, one simple approach is to use a list where the first elements are the inner ring and the last five elements are the outer ring in clockwise order.
Generating every possible rings can be easily done using itertools.permutations.
2. Check if each ring is valid.
To validate a "magic" gon ring, it is enough to check if all lines add up to the same number. The \( i \)-th line is the sum of the \( i \)-th element of the inner ring, the \( i + 1 \)-th element of the inner ring, and the \( i \)-th element of the outer ring. If all lines have the same sum, then the ring is valid. This is checked by verifying that the set of line sums has only one element.
From solution1.py:
def is_gon_valid(inner, outer):
return len(set(inner[i] + inner[(i + 1) % 5] + outer[i] for i in range(5))) == 1
3. Check if each ring is a 16-digit string.
The string representation of a ring is the concatenation of each line, starting with the lowest external node and reading clockwise. Each line is represented by the concatenation of the outer node, and the two inner nodes.
From solution1.py:
def ring_to_string(inner, outer):
start = outer.index(min(outer))
return "".join((str(outer[i % 5]) + str(inner[i % 5]) + str(inner[(i + 1) % 5]) for i in range(start, start + 5)))
Finding string of length 16 is trivial.
4. Find the maximum 16-digit string.
The maximum 16-digit string can be found using max built-in function, as it performs a lexicographical comparison.
The rest is to put it all together.
From solution1.py:
def magic_5_gon_ring():
all_gons = itertools.permutations(range(1, 11)) # Condition 1
valid_gons = filter(lambda gon: is_gon_valid(gon[:5], gon[5:]), all_gons) # Condition 2
string_gons = map(lambda gon: ring_to_string(gon[:5], gon[5:]), valid_gons)
string_gons = filter(lambda gon: len(gon) == 16, string_gons) # Condition 3
res = max(string_gons) # Condition 4
return res
Solution
6531031914842725
Totient maximum
Euler's Totient function, \( \phi(n) \) [sometimes called the phi function], is defined as the number of positive integers not exceeding n which are relatively prime to n. For example, as \( 1 \), \( 2 \), \( 4 \), \( 5 \), \( 7 \), and \( 8 \), are all less than or equal to nine and relatively prime to nine, \( \phi(9)=6 \).
$n$ Relatively Prime $\phi(n)$ $n/\phi(n)$ 2 1 1 2 3 1,2 2 1.5 4 1,3 2 2 5 1,2,3,4 4 1.25 6 1,5 2 3 7 1,2,3,4,5,6 6 1.1666... 8 1,3,5,7 4 2 9 1,2,4,5,7,8 6 1.5 10 1,3,7,9 4 2.5 It can be seen that \( n=6 \) produces a maximum \( \frac{n}{\phi(n)} \) for \( n\leq 10 \).
Find the value of \( n\leq 1,000,000 \) for which \( \frac{n}{\phi(n)} \) is a maximum.
Brute force
The problem is to find the value of \( n \) for which \( \frac{n}{\phi(n)} \) is a maximum.
The naive approach is to compute \( \phi(n) \) for all \( n \) up to \( 1,000,000 \) and then find the maximum value of \( \frac{n}{\phi(n)} \). \( \phi(n) \) can be computed by summing the count of coprimes numbers of \( n \) up to \( n - 1 \).
Two numbers are considered coprime if their greatest common divisor is \( 1 \), indicating that they have no common factors. Checking for coprime numbers can be done by verifying if there exists any number that is a factor of both numbers in the range from \( 1 \) to \( \min(a, b) \).
From solution1.py:
def are_coprime(a, b):
return not any(a % i == 0 and b % i == 0 for i in range(2, min(a, b) + 1))
Finally, the rest is to compute \( \frac{n}{\phi(n)} \) for all \( n \) up to \( 1,000,000 \) and find the maximum value.
From solution1.py:
def totient_maximum():
res = 0
res_n = 0
for n in range(2, 1000001):
totient = sum(are_coprime(n, i) for i in range(1, n))
res = max(res, n / totient)
if n / totient > res:
res = n / totient
res_n = n
return res_n
Caching totients
The current Brute force solution is inefficient due to its bottleneck is the computation of \( \phi(n) \).
The function are_coprime is called \( n \) times, and each call takes \( O(n) \) time, leading to a total runtime of \( O(n^3) \) for all \( \phi(n) \).
A more efficient solution involves using a similar process to the Sieve of Eratosthenes, where every multiple of a \( a \leq n \) is not coprime to \( n \). By employing this method, \( \phi(n) \) for all \( n \) can be computed in \( O(n \log(\log(n))) \) time.
From solution2.py:
def totient_list(n):
tlist = list(range(n))
for i in range(1, n):
p = tlist[i]
for j in range(2 * i, n, i):
tlist[j] -= p
return tlist
Furthermore, caching all totients enables the computation of \( \frac{n}{\phi(n)} \) for all \( n \) in linear time.
From solution2.py:
def totient_maximum(limit=1000001):
res = 0
res_n = 0
totatives = totient_list(limit)
for n in range(2, limit):
if n / totatives[n] > res:
res = n / totatives[n]
res_n = n
return res_n
Euler's totient function
The Euler's totient function is defined as \( \phi(n) \). There are several formulae for computing \( \phi(n) \), one of which is the following:
\[ \phi(n) = n \prod_{p \in \mathcal{P}} \left( 1 - \frac{1}{p} \right) \]
where \( \mathcal{P} \) is the set of prime factors of \( n \).
Remembering that the solution is \( n \) for which \( \frac{n}{\phi(n)} \) is a maximum, which is equivalent to finding \( n \) for which \( \frac{\phi(n)}{n} \) is a minimum, we can rewrite the above formula as
\[ \frac{\phi(n)}{n} = \prod_{p \in \mathcal{P}} \left( 1 - \frac{1}{p} \right) \]
Obviously, this is minimized when \( \mathcal{P} \) is large, therefore the solution is the number which has the largest number of prime factors.
In our case, \( n \leq 1000000 \), so the solution is \( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 = 510510 \).
Solution
510510
Totient permutation
Euler's Totient function, \( \varphi (n) \) [sometimes called the phi function], is used to determine the number of positive numbers less than or equal to \( n \) which are relatively prime to \( n \). For example, as \( 1 \), \( 2 \), \( 4 \), \( 5 \), \( 7 \), and \( 8 \), are all less than nine and relatively prime to nine, \( \varphi(9) = 6 \). The number \( 1 \) is considered to be relatively prime to every positive number, so \( \varphi(1) = 1 \)
Interestingly, \( \varphi(87109) = 79180 \), and it can be seen that \( 87109 \) is a permutation of \( 79180 \).
Find the value of \( n \), \( 1<n<10^7 \), for which \( \varphi(n) \) is a permutation of \( n \) and the ratio \( \frac{n}{\varphi(n)} \) produces a minimum.
Brute force
The problem is very similar to the Problem 0069 as it also involves Euler's totient function. This problem asks to find the value of \( n \) for which \( \frac{n}{\phi(n)} \) is minimal and \( n \) is a permutation of \( \phi(n) \).
Thanks to the Problem 0069, generating a list of totients is easy.
From solution1.py:
def totient_list(n):
tlist = list(range(n))
for i in range(1, n):
p = tlist[i]
for j in range(2 * i, n, i):
tlist[j] -= p
return tlist
Therefore, filtering every totient that is not a permutation of its index and finding the minimum ratio is all that is left to do.
From solution1.py:
def totient_permutation(limit=10000001):
totatives = totient_list(limit)
totatives = ((n, t) for n, t in enumerate(totatives) if sorted(str(n)) == sorted(str(t)) and n > 1)
return min(totatives, key=lambda x: x[0] / x[1])[0]
Euler's totient function
Recalling that \( \phi(n) = n(1 - \frac{1}{p_1})(1 - \frac{1}{p_2})\dots(1-\frac{1}{p_k}) \) with \( n = p_1^{e_1}p_2^{e_2}\dots p_k^{e_k} \). It is obvious that minimizing \( \frac{n}{\phi(n)} \) is equivalent to maximizing \( \phi(n) \).
To maximize \( \phi(n) \), it is ideal to choose \( n \) with as few prime factors as possible. Ideally, \( n \) should be a prime number, but it does not result with a permutation as \( \phi(n) = n - 1 \). Additionally, \( n \) can not be equal to \( p^k \) as \( n=p^k \) and \( \phi(n) = p^{k-1}(p-1) \) are not permutations of each other. This can be proven by working modulo 3, but since the proof is not relevant, it is assumed to be true.
Hence, a product of two primes should be chosen, where the two primes are as large as possible, close to each other, and to \( \sqrt{10^7} \). If no such prime pair exists, then a product of three primes should be chosen, and so on.
If \( a \) and \( b \) are permutations of each other, then \( a - b \) is a multiple of \( 9 \). Therefore, if \( n \) is a permutation of \( \phi(n) \), then \( n - \phi(n) = p_1 + p_2 -1 \) must be a multiple of \( 9 \). This property can be used to filter out totients that are not permutations of their index without having to compute the full check, which is computationally expensive.
To find the solution, it is sufficient to consider \( n \) as a product of two primes, so the code below does not consider products of more than two primes.
From solution2.py:
def totient_permutation(limit=10000001):
primes = list(sieve.primerange(2, 2 * int(limit**0.5)))
res = 0
ratio = float("inf")
for i in range(len(primes)):
for j in range(i):
if (primes[i] + primes[j] - 1) % 9 != 0:
continue
n = primes[i] * primes[j]
if n > limit:
break
t = (primes[i] - 1) * (primes[j] - 1)
if n / t < ratio and sorted(str(n)) == sorted(str(t)):
res = n
ratio = n / t
return res
While the most optimal iteration would involve iterating over all primes sorted by their distance to \( \sqrt{10^7} \), it is a more complex approach to implement and not worth the effort. Therefore, for simplicity, the primes are iterated over in ascending order, and the limit is arbitrarily set to \( 2\sqrt{10^7} \).
Solution
8319823
Ordered fractions
Consider the fraction, \( \frac{n}{d} \), where n and d are positive integers. If \(n < d\) and \( HCF(n,d) = 1 \), it is called a reduced proper fraction.
If we list the set of reduced proper fractions for \( d ≤ 8 \) in ascending order of size, we get:
\[ \frac{1}{8},\frac{1}{7},\frac{1}{6},\frac{1}{5},\frac{1}{4},\frac{2}{7},\frac{1}{3},\frac{3}{8},\mathbf{\frac{2}{5}},\frac{3}{7},\frac{1}{2},\frac{4}{7},\frac{3}{5},\frac{5}{8},\frac{2}{3},\frac{5}{7},\frac{3}{4},\frac{4}{5},\frac{5}{6},\frac{6}{7},\frac{7}{8} \]
It can be seen that \( \frac{2}{5} \) is the fraction immediately to the left of \( \frac{3}{7} \).
By listing the set of reduced proper fractions for d ≤ \( 1,000,000 \) in ascending order of size, find the numerator of the fraction immediately to the left of \( \frac{3}{7} \).
Brute force
The problem is to find the maximum reduced proper fraction \( \frac{n}{d} < \frac{3}{7} \) with \( n < d \leq 1000000 \).
The brute force approach iterate over every \( n \) and \( d \) and find the maximum fraction that satisfies the condition. There is no need to reduce the fraction since the iteration is ascending and the reduced fraction will be found first.
From solution1.py:
def ordered_fractions(limit=1000001):
res = 0, 1
for n in range(1, limit):
for d in range(1, limit):
if res[0] / res[1] < n / d < 3 / 7:
res = n, d
return res[0]
Farey sequence
The Brute force is inefficient because the iterations are not in ascending order of \( \frac{n}{d} \). On way to optimize the solution would be to increase \( n \) until \( \frac{n}{d} > \frac{3}{7} \) and then decrease \( d \) until \( \frac{n}{d} < \frac{3}{7} \), stopping just before either condition is met. However, a much better solution involves using Farey sequences.
A Farey sequence is a list of all sorted reduced proper fractions between 0 and 1.
The Farey sequence is constructed by starting with the two fractions \( \frac{0}{1} \) and \( \frac{1}{1} \) and then inserting the mediant of every adjacent pair of fractions. Each new fraction \( \frac{a + c}{b + d} \) is inserted between \( \frac{a}{b} \) and \( \frac{c}{d} \).
In this problem, we know that \( \frac{2}{5} < \frac{3}{7} \). Therefore, the solution can be obtained by finding the largest fraction in the Farey sequence with a denominator less than or equal to 1,000,000.
From solution2.py:
def ordered_fractions(limit=1000000):
a, b = 2, 5
c, d = 3, 7
while b + d <= limit:
a, b = a + c, b + d
return a
We can further optimize this solution by noting that \( b \) is always updated by adding \( d \) until \( b + d > 1000000 \). This operation is performed \( k = \lfloor \frac{1000000 - b}{d} \rfloor \) times, so the denominator of the largest fraction is \( b + kd \) and the numerator is \( a + kc \). For this problem, the largest numerator is \( 2 + 3\lfloor \frac{1000000 - 5}{7} \rfloor = 428570 \).
Solution
428570
Counting fractions
Consider the fraction, \( \frac{n}{d} \), where n and d are positive integers. If \(n < d\) and \( HCF(n,d) = 1\), it is called a reduced proper fraction.
If we list the set of reduced proper fractions for \( d \leq 8 \) in ascending order of size, we get:
\[ \frac{1}{8}, \frac{1}{7}, \frac{1}{6}, \frac{1}{5}, \frac{1}{4}, \frac{2}{7}, \frac{1}{3}, \frac{3}{8}, \frac{2}{5}, \frac{3}{7}, \frac{1}{2}, \frac{4}{7}, \frac{3}{5}, \frac{5}{8}, \frac{2}{3}, \frac{5}{7}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \frac{6}{7}, \frac{7}{8} \]
It can be seen that there are \( 21 \) elements in this set.
How many elements would be contained in the set of reduced proper fractions for \( d \leq 1,000,000 \) ?
Brute force
The Problem 0071 teach us that Farey sequences are useful to solve problem involving HCF. Given two fractions \( \frac{a}{b} \) and \( \frac{c}{d} \), it is possible to determine the mediant \( \frac{a+c}{b+d} \).
In this problem, the first two terms are \( \frac{0}{1} \) and \( \frac{1}{n} \), with \( n=1000000 \). The next term \( \frac{p}{q} \) can be found using the first two terms \( \frac{a}{b} \) and \( \frac{c}{d} \):
\[ \frac{a + p}{b + q} = \frac{c}{d} \]
Since \( \frac{c}{d} \) is in lowest terms, there exists an integer \( k \) such that \( a + p = kc \) and \( b + q = kd \). Also, \( \frac{p}{q} - \frac{c}{d} = \frac{cb - da}{d(kd - b)} \) so the larger the value of \( k \), the closer \( \frac{p}{q} \) is to \( \frac{c}{d} \). The next term \( \frac{p}{q} \) is the one with the largest \( k \) such that \( kd - b \leq n \Leftrightarrow k \leq \frac{n + b}{d} \). This gives the following recurrence relation:
\[ p = \left\lfloor \frac{n + b}{d} \right\rfloor c - a \\ q = \left\lfloor \frac{n + b}{d} \right\rfloor d - b \]
This relation can be used to generate all the terms of the Farey sequence, in our case, counting the number of terms is enough to solve the problem.
From solution1.py:
def counting_fractions(n=1000001):
a, b, c, d = 0, 1, 1, n
res = 0
while c <= n:
k = (n + b) // d
a, b, c, d = c, d, k * c - a, k * d - b
res += 1
return res
Farey sequence and Euler's totient function
The Brute force solution is inefficient due to the large number of terms in the Farey sequence. However, it is still possible to use the Farey sequence to solve this problem efficiently. A Farey sequence of order \( n \) is defined as the sequence of irreducible fractions between \( 0 \) and \( 1 \) whose denominators do not exceed \( n \). The number of terms in the Farey sequence is given by the formula \( \left | F_n \right | = \left | F_{n-1} \right | + \phi(n) \), where \( \phi(n) \) is Euler's totient function. Using the fact that \( \left | F_1 \right | = 2 \), then \( \left | F_n \right | = 1 + \sum_{k=1}^{n} \phi(k) \).
The sum of the totient function is something already done in Problem 0069. In this problem, \( \frac{0}{1} \) and \( \frac{1}{n} \) are not counted, so the answer is \( \left | F_n \right | = \sum_{k=1}^{n} \phi(k) - 1 \).
From solution2.py:
def counting_fractions(n=1000000):
tlist = list(range(n + 1))
for i in range(1, n + 1):
p = tlist[i]
for j in range(2 * i, n + 1, i):
tlist[j] -= p
return sum(tlist) - 1
Solution
303963552391
Counting fractions in a range
Consider the fraction, \( \frac{n}{d} \), where n and d are positive integers. If \( n < d \) and \( HCF(n,d) = 1 \), it is called a reduced proper fraction.
If we list the set of reduced proper fractions for \( d \leq 8 \) in ascending order of size, we get:
\[ \frac{1}{8}, \frac{1}{7}, \frac{1}{6}, \frac{1}{5}, \frac{1}{4}, \frac{2}{7}, \frac{1}{3}, \mathbf{\frac{3}{8}, \frac{2}{5}, \frac{3}{7}}, \frac{1}{2}, \frac{4}{7}, \frac{3}{5}, \frac{5}{8}, \frac{2}{3}, \frac{5}{7}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \frac{6}{7}, \frac{7}{8} \]
It can be seen that there are \( 3 \) fractions between \( \frac{1}{3} \) and \( \frac{1}{2} \).
How many fractions lie between \( \frac{1}{3} \) and \( \frac{1}{2} \) in the sorted set of reduced proper fractions for \( d \leq 12,000 \)?
Brute force
The problem is to find the number of reduced proper fractions \( \frac{n}{d} \) such that \( \frac{1}{3} < \frac{n}{d} < \frac{1}{2} \) and \( n \) and \( d \) are coprime. A brute force solution generates all Farey sequences between \( \frac{1}{3} \) and \( \frac{1}{2} \) and counting the number of fractions in each sequence.
The Stern-Brocot tree can be used to generate Farey sequences. Starting from two adjacent fractions \( \frac{a}{b} \) and \( \frac{c}{d} \), the mediant \( \frac{a+c}{b+d} \) is also in the Farey sequence. This process can be repeated with the left fraction and the mediant, and the right fraction and the mediant, and so on.
From solution1.py:
def stern_brocot_tree(a, b, c, d):
if b + d > 12000:
return 0
return 1 + stern_brocot_tree(a, b, a + c, b + d) + stern_brocot_tree(a + c, b + d, c, d)
To solve the problem, the rest is to initialize the tree with the fractions \( \frac{1}{3} \) and \( \frac{1}{2} \), and count the number of fractions in the Farey sequence between them.
From solution1.py:
def counting_fractions_in_a_range():
return stern_brocot_tree(1, 3, 1, 2)
It is worth noting that the Python default recursion limit may need to be increased for this solution to work.
Solution
7295372
Digit factorial chains
The number \( 145 \) is well known for the property that the sum of the factorial of its digits is equal to \( 145 \):
\[ 1! + 4! + 5! = 1 + 24 + 120 = 145 \]
Perhaps less well known is \( 169 \), in that it produces the longest chain of numbers that link back to \( 169 \); it turns out that there are only three such loops that exist:
\[ \begin{align} &169 \rightarrow 363601 \rightarrow 1454 \rightarrow 169\\ &871 \rightarrow 45361 \rightarrow 871\\ &872 \rightarrow 45362 \rightarrow 872 \end{align} \]
It is not difficult to prove that EVERY starting number will eventually get stuck in a loop. For example,
\[ \begin{align} &69 \rightarrow 363600 \rightarrow 1454 \rightarrow 169 \rightarrow 363601 (\rightarrow 1454)\\ &78 \rightarrow 45360 \rightarrow 871 \rightarrow 45361 (\rightarrow 871)\\ &540 \rightarrow 145 (\rightarrow 145) \end{align} \]
Starting with \( 69 \) produces a chain of five non-repeating terms, but the longest non-repeating chain with a starting number below one million is sixty terms.
How many chains, with a starting number below one million, contain exactly sixty non-repeating terms?
Brute force
The objective is to determine the number of chains with a starting number below one million that consist of exactly sixty non-repeating terms.
A straightforward approach is to iterate through each number below one million, calculate the chain using a set to track the terms already seen, and increment the count if the chain has exactly sixty terms.
From solution1.py:
def digit_factorial_chains():
res = 0
factorials = [1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
for i in range(1, 1000000):
found = set()
while i not in found:
found.add(i)
i = sum([factorials[int(digit)] for digit in str(i)])
if len(found) == 60:
res += 1
return res
Caching the chain
The main drawback of the Brute force approach is that it recalculates the whole chain for each number. One way to improve the performance is to cache the length of the chain for each number of the chain.
This approach use a dictionary to store the chain length for each number. Instead of using a set, a list is preferred to keep track of the position of each number in the chain. For each number below one million, the chain is computed as before. However, if the current number already exists in the dictionary, indicating that its length is already known, the computation can be terminated prematurely.
Upon completion of the chain, every number in the current chain is added to the dictionary. The value assigned to each number is equal to its position in the chain plus the length of the final element in the chain. If the final element is not present in the dictionary, its length is set to zero.
From solution2.py:
def digit_factorial_chains():
res = 0
factorials = [1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
cache = {}
for i in range(1, 1000000):
found = []
while i not in found and i not in cache:
found.append(i)
i = sum([factorials[int(digit)] for digit in str(i)])
for j, v in enumerate(found):
cache[v] = len(found) - j + cache.get(i, 0)
if cache[v] == 60:
res += 1
return res
Solution
402
Singular Integer Right Triangles
It turns out that \( 12 \)cm is the smallest length of wire that can be bent to form an integer sided right angle triangle in exactly one way, but there are many more examples.
- \( 12 \) cm: \( (3,4,5) \)
- \( 24 \) cm: \( (6,8,10) \)
- \( 30 \) cm: \( (5,12,13) \)
- \( 36 \) cm: \( (9,12,15) \)
- \( 40 \) cm: \( (8,15,17) \)
- \( 48 \) cm: \( (12,16,20) \)
In contrast, some lengths of wire, like \( 20 \) cm, cannot be bent to form an integer sided right angle triangle, and other lengths allow more than one solution to be found; for example, using \( 120 \) cm it is possible to form exactly three different integer sided right angle triangles.
- \( 120 \) cm: \( (30,40,50), (20,48,52), (24,45,51) \)
Given that \( L \) is the length of the wire, for how many values of \( L \le 1,500,000 \) can exactly one integer sided right angle triangle be formed?
Tree of primitive Pythagorean triples
The objective is to determine the number of Pythagorean triples that yield a unique perimeter.
Thanks to Problem 0039, the process of computing all pythagorean triples becomes straightforward
We can actually use the code in the Tree of primitive Pythagorean triples solution. However, we need to replace the return statement in order to count the number of perimeter that can only be formed in one possible way.
From solution1.py:
def compute_all_pythagorean_triples(results, max_p, abc):
curr_p = sum(abc)
if curr_p < max_p:
for perimeter in range(curr_p, max_p, curr_p):
results[perimeter] += 1
compute_all_pythagorean_triples(results, max_p, A @ abc)
compute_all_pythagorean_triples(results, max_p, B @ abc)
compute_all_pythagorean_triples(results, max_p, C @ abc)
From solution1.py:
def singular_integer_right_triangles():
results = defaultdict(int)
compute_all_pythagorean_triples(results, 1500000, np.array([3, 4, 5]))
return sum(filter(lambda x: x == 1, results.values()))
Solution
161667
Counting Summations
It is possible to write five as a sum in exactly six different ways:
How many different ways can one hundred be written as a sum of at least two positive integers?
Dynamic programming
The problems is a variation of the Coins sums problem. The only difference is the number of coins, which is now 1, 2, 3, ..., 99.
From solution1.py:
def counting_summations(n=100):
numbers = list(range(1, n))
cache = [1] + [0] * n
for number in numbers:
for i in range(number, n + 1):
cache[i] += cache[i - number]
return cache[-1]
Solution
190569291
Prime Summations
It is possible to write ten as the sum of primes in exactly five different ways:
What is the first value which can be written as the sum of primes in over five thousand different ways?
Dynamic programming
The problems is a variation of the Coins sums problem. The only difference is the number of coins, which is now prime numbers. With trial and error, setting the limit to 100 is enough to get the correct answer.
From solution1.py:
def prime_summations(n=100):
numbers = list(sieve.primerange(1, n + 1))
cache = [1] + [0] * n
for number in numbers:
for i in range(number, n + 1):
cache[i] += cache[i - number]
return next(i for i, x in enumerate(cache) if x > 5000)
Solution
71
Coin Partitions
Let \( p(n) \) represent the number of different ways in which \( n \) coins can be separated into piles. For example, five coins can be separated into piles in exactly seven different ways, so \( p(5) = 7\).
\[ \begin{align} &OOOOO\\ &OOOO\ \ O\\ &OOO\ \ OO\\ &OOO\ \ O\ \ O\\ &OO\ \ OO\ \ O\\ &OO\ \ O\ \ O\ \ O\\ &O\ \ O\ \ O\ \ O\ \ O \end{align} \]
Find the least value of n for which \( p(n) \) is divisible by one million.
Dynamic programming is hidden recursion problem
Another coins problem, another dynamic programming solution ! This solution comes naturally when you try to find the different ways \( n \) coins can be separated into piles.
If you were to solve this by hand, you will start with piles of size 1, then of size 2 and one, then of size 3, 2 and one, and so on. The goal is to find a recurrence relation between \( p(n, k) \) and \( p(n, k+1) \) where \( p(n, k) \) denotes the number of ways to partition \( n \) coins into piles of size \( k \) or less.
Consider this table:
| n k | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 | 2 |
| 3 | 1 | 2 | 3 | 3 | 3 |
| 4 | 1 | 3 | 4 | 5 | 5 |
| 5 | 1 | 3 | 5 | 6 | 7 |
Each cell \( (n, k) \) represents the number of ways to partition \( n \) coins into piles of size \( k \) or less. The recurrence relation closely resembles the of for the coin sums problem:
\[ p(n, k) = p(n, k-1) + p(n-k, k) \]
The first term represents the number of ways to partition \( n \) coins into piles of size \( k-1 \) or less, while the second term represents the number of ways to separate \( n \) coins using at least one pile of size \( k \). Finally, the base cases are \( p(0, k) = 1 \) and \( p(n, k) = p(n, k -1) \) if \( n < k \).
The rest of the code is relatively straightforward if you understand that you can compute each column of the table one after the other. Furthermore, since you only care about the remainder of the division by \( 10^6 \), you can use the modulo operator to keep the numbers small.
From solution1.py:
def coin_partitions(limit=100000):
divisible_by = 1000000
cache = [1] * (limit + 1)
for l in range(2, limit + 1):
cache[l] = (cache[l] + 1) % divisible_by
if cache[l] == 0:
return l
for n in range(l + 1, limit + 1):
cache[n] = (cache[n] + cache[n - l]) % divisible_by
Euler partition function
The partition function \( p(n) \) represents the number of ways to partition \( n \) coins into piles of size \( k \) or less, that is, the function we are looking for. Using Euler's recurrence relation, we can calculate \( p(n) \) for any \( n \): \[ \begin{aligned} p(n) &= \sum_{k\in\mathbb{Z}\backslash\{0\}}^{\infty} (-1)^{k+1} p \left( n - \frac{k(3k-1)}{2} \right)\\ &= \sum_{k=1}^{\infty} (-1)^{k+1} \left[ p \left( n - \frac{k(3k-1)}{2} \right) + p \left( n - \frac{k(3k+1)}{2} \right) \right] \end{aligned} \]
This summation is over all nonzero integers \( k \), but since \( p(n) = 0 \) for \( n < 0 \), the series has only finitely many nonzero terms, and can be computed in a finite amount of time.
Using python mutable variables as a cache for previously computed \( p(n) \) values, we can compute \( p(n) \) much more effeciently than the last solution.
From solution2.py:
def p(n, cache={}):
if n in cache:
return cache[n]
if n < 0:
return 0
if n < 2:
return 1
cum_sum = 0
for k in range(1, n + 1):
n1 = n - k * (3 * k - 1) // 2
n2 = n - k * (3 * k + 1) // 2
cum_sum += (-1) ** (k + 1) * (p(n1, cache) + p(n2, cache))
if n1 <= 0: # n1 < n2, no need to check both
break
cache[n] = cum_sum % 1000000
return cache[n]
The rest is to find the smallest \( n \) such that \( p(n) \) is divisible by \( 10^6 \).
From solution2.py:
def coin_partitions(n=1000000):
for i in itertools.count(0):
r = p(i)
if r % n == 0:
return i
Solution
71
Passcode Derivation
A common security method used for online banking is to ask the user for three random characters from a passcode. For example, if the passcode was \( 531278 \), they may ask for the \( 2 \)nd, \( 3 \)rd, and \( 5 \)th characters; the expected reply would be: \( 317 \).
The text file, keylog.txt, contains fifty successful login attempts.
Given that the three characters are always asked for in order, analyse the file so as to determine the shortest possible secret passcode of unknown length.
Topological sorting
Problem:
We need to to find the shortest passcode based on a series of samples containing three random characters chosen in order.
Understanding the problem
For example, if the samples are \( 145 \), \( 456\) and \( 146 \), we can infer certain order constraints, like \( 1 \) must be before \( 4 \), \( 4 \) before \( 5 \), and so on. We also know that \( 1 \) is before \( 5 \), but it would be redundant since we already know that \( 1 \) is before \( 4 \) and \( 4 \) is before \( 5 \).
We can represent these constraints as a directed graph, where the nodes are the characters and the edges describe the constraints, i.e. if there is an edge \( a \rightarrow b \), then \( a \) is before \( b \). For the previous example, the graph would be:
From this graph, it's clear that the shortest passcode is \( 1456 \). But what if the graph was more complex? If it was, we would need some algorithm to find the solution, and that is where topological sorting comes in handy.
Solution
The first step is to read the file:
From read_file.py:
def read_file(filename):
with open(filename, "r") as file:
return file.read().splitlines()
Then, we can compute the graph. I chose to represent the graph as a dictionary of sets, where the keys are the nodes and the values the connected nodes. Using the previous example, the graph would be represented as:
{
'1': {'4'},
'4': {'5', '6'},
'5': {'6'},
}
From solution1.py:
def compute_graph(char):
graph = defaultdict(set)
for a, b, c in char:
graph[a].add(b)
graph[b].add(c)
return graph
Using some visualization, here's what the graph looks like with the real data:
Quite tentacular, but we can still guess the passcode: \( 73162890 \). For the topological sorting, I've opted to use depth-first search since it's the easiest to implement.
From solution1.py:
def topological_sort(graph):
marked = set()
result = []
def dfs(node):
if node not in marked:
# Using defaultdict requires us to check if the node is in the graph
# to prevent errors during iteration caused by unintentional key creation.
if node in graph:
for neighbour in graph[node]:
dfs(neighbour)
marked.add(node)
result.insert(0, node)
for node in graph:
dfs(node)
return result
Finally, we merge everything together to obtain the solution:
From solution1.py:
def passcode_derivation(filename="keylog.txt"):
chars = read_file(filename)
graph = compute_graph(chars)
passcode = topological_sort(graph)
return "".join(passcode)
The passcode is indeed \( 73162890 \).
If you understood the solution, you might have noticed that we assumed that the graph is acyclic, meaning it has no cycles. In our case, this implies that there is no redundant numbers in the passcode. If there were cycles, finding the passcode would be more challenging... Maybe it will be the subject of another solution?
Solution
73162890
Square Root Digital Expansion
It is well known that if the square root of a natural number is not an integer, then it is irrational. The decimal expansion of such square roots is infinite without any repeating pattern at all.
The square root of two is \( 1.41421356237309504880 \cdots \), and the digital sum of the first one hundred decimal digits is \( 475 \).
For the first one hundred natural numbers, find the total of the digital sums of the first one hundred decimal digits for all the irrational square roots.
Square roots by subtraction
Problem
We need to find the sum of the first one hundred decimal digits of the square roots of the first one hundred natural numbers.
Understanding the problem
The problem is not difficult to understand, the challenge lies in determining the decimal digits of the square roots.
Solution
We could use Python's decimal module, but that would not be very interesting. Instead, we will use an algorithm that computes square roots digit by digit. As usual, Wikipedia has plenty to offer. I chose the subtraction method from Jarvis Frazer as it seemed the easiest to implement.
Let \( a = 5n \) and \( b = 5 \), where \( n \) is the number whose square root we want to compute. We follow the following rules:
\[ \begin{align} &(R1) \ If\ a\geqslant b,\ replace\ a\ with\ a-b,\ and\ add\ 10\ to\ b.\\ &(R2) \ If\ a< b,\ add\ two\ zeroes\ to\ the\ end\ of\ a,\ and\ add\ a\ zero\ to\ b\ just\ before\ the\ final\ digit. \end{align} \]
The process is repeated until \( b \), which approximates the square root of \( n \), is greater than \( 10^{p + 1} \) where \( p \) is the precision. In our case, \( p = 100 \). The only special case is when \( a = 0 \), indicating that \( n \) is a perfect square, which si not considered in this problem.
The code is pretty straightforward:
From solution1.py:
def square_root(n):
a, b = 5 * n, 5
while b < 10**101:
if a >= b:
a -= b
b += 10
else:
# Perfect square
if a == 0:
return 0
a *= 100
b = (b // 10) * 100 + 5
return b
To obtain the result, we just have to sum the digits of the first one hundred square roots:
From solution1.py:
def square_root_digital_expansion():
return sum(int(c) for n in range(1, 101) for c in str(square_root(n))[:100])
Solution
40886
Path Sum: Two Ways
In the \( 5 \) by \( 5 \) matrix below, the minimal path sum from the top left to the bottom right, by only moving to the right and down, is indicated in bold red and is equal to \( 2427 \).
\[ \begin{pmatrix} \color{red}{131} & 673 & 234 & 103 & 18\\ \color{red}{201} & \color{red}{96} & \color{red}{342} & 965 & 150\\ 630 & 803 & \color{red}{746} & \color{red}{422} & 111\\ 537 & 699 & 497 & \color{red}{121} & 956\\ 805 & 732 & 524 & \color{red}{37} & \color{red}{331}\\ \end{pmatrix} \]
Find the minimal path sum from the top left to the bottom right by only moving right and down in matrix.txt (right click and "Save Link\( / \)Target As\( ... \)"), a \( 31 \)K text file containing an \( 80 \) by \( 80 \) matrix.
Dynamic programming
Problem
This problem is very similar to Problem 18 and Problem 67 However, instead of a triangular structure, we are dealing with square matrix. The objective is to find the path from the top left corner to the bottom right corner with the smallest sum.
Understanding the problem
We can use dynamic programming just like in Problem 18 and Problem 67. Starting from the top left corner, we iterate line by line to the bottom right corner. At each cell, we find which neighboring cell (above or to the left) has the smallest sum and add it to the current cell. This process is repeated until we reach the bottom right corner.
Solution
The first step is to read the file and store the matrix in a list of lists.
From read_file.py:
def read_file(filename):
with open(filename, "r") as file:
return [[int(x) for x in line.split(",")] for line in file.read().splitlines()]
The algorithm is straightforward, we just need to take care of the edges cases where we can't go up or left.
From solution1.py:
def path_sum_two_ways(filename="matrix.txt"):
matrix = read_file(filename)
for i in range(len(matrix[0])):
for j in range(len(matrix[0])):
if i == 0 and j == 0:
continue
elif i == 0:
matrix[i][j] += matrix[i][j - 1]
elif j == 0:
matrix[i][j] += matrix[i - 1][j]
else:
matrix[i][j] += min(matrix[i - 1][j], matrix[i][j - 1])
return matrix[-1][-1]
Solution
427337
Path Sum: Three Ways
NOTE: This problem is a more challenging version of Problem 81.
The minimal path sum in the \( 5 \) by \( 5 \) matrix below, by starting in any cell in the left column and finishing in any cell in the right column, and only moving up, down, and right, is indicated in red and bold; the sum is equal to \( 994 \).
\[ \begin{pmatrix} 131 & 673 & \color{red}{234} & \color{red}{103} & \color{red}{18}\\ \color{red}{201} & \color{red}{96} & \color{red}{342} & 965 & 150\\ 630 & 803 & 746 & 422 & 111\\ 537 & 699 & 497 & 121 & 956\\ 805 & 732 & 524 & 37 & 331\\ \end{pmatrix} \]
Find the minimal path sum from the left column to the right column in matrix.txt (right click and "Save Link\( / \)Target As\( ... \)"), a \( 31 \)K text file containing an \( 80 \) by \( 80 \) matrix.
Dynamic programming
Problem
The problem is the exact same as Problem 81, but this time, we can go up.
Understanding the solution
In this problem, moving up and down multiple times within the same column is allowed. However, the optimal path won't go both up and down within the same column. That would be wasting steps because every cell has a positive value. So if we iterate from top to bottom, we only need to know if the cell above has been updated. Similarly, if we iterate from bottom to top, we only need to know if the cell below has been updated.
Now, let's take a look at this example where we iterate from left to right for the first column:
\[ \begin{bmatrix} \color{red}{1} & 1 & 10\\ \color{red}{10} & 1 & 10\\ \color{red}{15} & 1 & 1 \end{bmatrix} \Longrightarrow \begin{bmatrix} 1 & \color{red}{2} & 10\\ 10 & \color{red}{11} & 10\\ 15 & \color{red}{16} & 1 \end{bmatrix}\\ \]
Nothing fancy here; we add the left cell's value to the current cell. Now, let's iterate from top to bottom for this column, updating the green cell:
\[ \begin{bmatrix} 1 & \color{red}{2} & 10\\ 10 & \color{green}{11} & 10\\ 15 & \color{red}{16} & 1 \end{bmatrix} \rightarrow (\color{red}{2} + 1) < \color{green}{11}\rightarrow \begin{bmatrix} 1 & \color{red}{2} & 10\\ 10 & \color{red}{3} & 10\\ 15 & \color{green}{16} & 1 \end{bmatrix} \rightarrow (\color{red}{3} + 1) < \color{green}{16}\rightarrow \begin{bmatrix} 1 & \color{red}{2} & 10\\ 10 & \color{red}{3} & 10\\ 15 & \color{red}{4} & 1 \end{bmatrix}\ \ \]
During the update, we're comparing the current cell's updated value with the above cell updated value plus the current cell's initial value. For this case, \( \color{green}{11} \) is compared with \( \color{red}{2} + 1 \). Keep repeating this process until you reach the column's bottom, then do the same from bottom to top:
\[ \begin{bmatrix} 1 & \color{red}{2} & 10\\ 10 & \color{green}{3} & 10\\ 15 & \color{red}{4} & 1 \end{bmatrix} \rightarrow (\color{red}{4} + 1) > \color{green}{3}\rightarrow \begin{bmatrix} 1 & \color{green}{2} & 10\\ 10 & \color{red}{3} & 10\\ 15 & \color{red}{4} & 1 \end{bmatrix} \rightarrow (\color{red}{3} + 1) > \color{green}{2}\rightarrow \begin{bmatrix} 1 & \color{red}{2} & 10\\ 10 & \color{red}{3} & 10\\ 15 & \color{red}{4} & 1 \end{bmatrix}\ \ \]
Implementation
The first step is to read the file and store the matrix, in this case, in a list of lists.
From read_file.py:
def read_file(filename):
with open(filename, "r") as file:
return [[int(x) for x in line.split(",")] for line in file.read().splitlines()]
The main challenge is handling the top-to-bottom and bottom-to-top iterations. Since we need to keep track of both the updated columns and initial columns, updating the matrix in place won't work. Instead, we can create a copy of the first column that will represent the updated values of the current column's smallest path.
So, when updating from left to right, we simply add to this copy the value of the initial cell of the right column. When updating from top to bottom, we compare the updated value of the current cell with the updated value of the cell above plus the initial value of the current cell. The process is the same for the bottom-to-top iteration.
From solution1.py:
def path_sum_three_ways(filename=".txt"):
rows = read_file(filename)
current = [r[0] for r in rows]
for x in range(1, len(rows[0])):
for y in range(len(rows)): # Left to right
current[y] += rows[y][x]
print(current)
for y in range(1, len(rows)): # Top to bottom
current[y] = min(current[y], current[y - 1] + rows[y][x])
for y in range(len(rows) - 2, -1, -1): # Bottom to top
current[y] = min(current[y], current[y + 1] + rows[y][x])
return min(current)
The answer is the minimum value of the copied column after we have iterated through the whole matrix.
Solution
260324
Path Sum: Four Ways
NOTE: This problem is a significantly more challenging version of Problem 81.
In the \( 5 \) by \( 5 \) matrix below, the minimal path sum from the top left to the bottom right, by moving left, right, up, and down, is indicated in bold red and is equal to \( 2297 \).
\[ \begin{pmatrix} \color{red}{131} & 673 & \color{red}{234} & \color{red}{103} & \color{red}{18}\\ \color{red}{201} & \color{red}{96} & \color{red}{342} & 965 & \color{red}{150}\\ 630 & 803 & 746 & \color{red}{422} & \color{red}{111}\\ 537 & 699 & 497 & \color{red}{121} & 956\\ 805 & 732 & 524 & \color{red}{37} & \color{red}{331}\\ \end{pmatrix} \]
Find the minimal path sum from the top left to the bottom right by moving left, right, up, and down in matrix.txt (right click and "Save Link\( / \)Target As\( ... \)"), a \( 31 \)K text file containing an gc\( 80 \) by \( 80 \) matrix.
Breadth-first search
Problem
The problem is the exact same as Problem 81 and Problem 82, but this time, we can go everywhere.
Grasping the solution
Because of this freedom of movement, we can not use the same approach as before, so let's explore other options. If we try to solve this problem with pen and paper, we would start from the top left corner, updating cells one by one just as follows:
In this example, green cells are currently being updated, red ones have been updated, and blue cells, while updated previously, are being updated again.
\[ \begin{align} &\begin{pmatrix} \color{green}{131} & 673 & 234 & 103 & 18\\ 201 & 96 & 342 & 965 & 150\\ 630 & 803 & 746 & 422 & 111\\ 537 & 699 & 497 & 121 & 956\\ 805 & 732 & 524 & 37 & 331\\ \end{pmatrix} \rightarrow \begin{pmatrix} \color{red}{131} & \color{green}{804} & 234 & 103 & 18\\ \color{green}{332} & 96 & 342 & 965 & 150\\ 630 & 803 & 746 & 422 & 111\\ 537 & 699 & 497 & 121 & 956\\ 805 & 732 & 524 & 37 & 331\\ \end{pmatrix} \rightarrow\\ &\begin{pmatrix} \color{red}{131} & \color{red}{804} & \color{green}{1035} & 103 & 18\\ \color{red}{332} & \color{green}{428} & 342 & 965 & 150\\ \color{green}{962} & 803 & 746 & 422 & 111\\ 537 & 699 & 497 & 121 & 956\\ 805 & 732 & 524 & 37 & 331\\ \end{pmatrix} \rightarrow \begin{pmatrix} \color{red}{131} & \color{red}{804} & \color{red}{1035} & \color{green}{1138} & 18\\ \color{red}{332} & \color{red}{428} & \color{green}{770} & 965 & 150\\ \color{red}{962} & \color{green}{1231} & 746 & 422 & 111\\ \color{green}{1499} & 699 & 497 & 121 & 956\\ 805 & 732 & 524 & 37 & 331\\ \end{pmatrix} \rightarrow\\ &\begin{pmatrix} \color{red}{131} & \color{red}{804} & \color{blue}{1004} & \color{red}{1138} & \color{green}{1156}\\ \color{red}{332} & \color{red}{428} & \color{red}{770} & \color{green}{1735} & 150\\ \color{red}{962} & \color{red}{1231} & \color{green}{1516} & 422 & 111\\ \color{red}{1499} & \color{green}{1930} & 497 & 121 & 956\\ \color{green}{2304} & 732 & 524 & 37 & 331\\ \end{pmatrix} \rightarrow \dots \end{align} \]
Notice that the blue cell is udpated twice. If we were solving this by hand, we would update its neighbors once more. Continuing this process leads us to the bottom right corner. Basically, its like a breadth-first search but with a twist: if a cell is being updated again, we revisit its neighbors (unlike traditional BFS, where nodes are not revisited). Moreover, we know that there will not be any cycles, so we can terminate the algorithm in a finite number of steps.
Implementation
The first step is to read the file and store the matrix, in this case, in a list of lists.
From read_file.py:
def read_file(filename):
with open(filename, "r") as file:
return [[int(x) for x in line.split(",")] for line in file.read().splitlines()]
When updating the blue cell in the example, we compared the updated value of the blue cell \( (1035) \) with the initial value of the blue cell \( (234) \) plus the updated value of its neighbor \( (770) \). To implement this, we need to know both the initial value and the updated value of each cell. A straightforward solution is to create a copy of the matrix where each cell is initialized with the maximum value, indicating that it hasn't been updated it yet.
We have two matrixes: the initial matrix \( I \) and the updated matrix \( U \). For each cell \( (i, j) \), we update its neighbor \( (ni, nj) \) to the minimum between its current value and the sum of the current cell \( (i, j) \) in the updated matrix and the the neighbor cell \( (ni, nj) \) in the initial matrix: \[ U(ni, nj) = \min \left( U(ni, nj), U(i, j) + I(ni, nj) \right ) \] As the updated matrix is initialized with the maximum value, it ensures that non-updated neighbors will always have values greater than other paths. Every time a neighbor is updated, we add it to a queue so we can update its neighbors later. We continue this process until the queue is empty, signifying that the updated matrix has stabilized.
From solution1.py:
def bfs(matrix, source):
updated = [[float("inf") for _ in range(len(matrix[0]))] for _ in range(len(matrix))]
updated[0][0] = matrix[0][0]
queue = [source]
while queue:
i, j = queue.pop(0)
for x, y in [(i, j + 1), (i, j - 1), (i + 1, j), (i - 1, j)]:
if 0 <= x < len(matrix) and 0 <= y < len(matrix[0]):
alt = updated[i][j] + matrix[x][y]
if alt < updated[x][y]:
updated[x][y] = alt
queue.append((x, y))
return updated
The last step is to return the value of the bottom right corner.
From solution1.py:
def path_sum_four_ways(filename="matrix.txt"):
matrix = read_file(filename)
return dijkstra(matrix, (0, 0), (len(matrix) - 1, len(matrix[0]) - 1))[-1][-1]
Dijkstra's algorithm
Problem
The problem is the exact same as Problem 81 and Problem 82, but this time, we can go everywhere.
Grasping the solution
We can enhance our previous solution by using a more efficient algorithm. The main drawback was the order in which we visited the nodes: none. Instead, we could prioritize cells wth the lowest values, as they are more likely to be part of the shortest path. This is exactly what Dijkstra's algorithm does.
Implementation
The first step is to read the file and store the matrix, in this case, in a list of lists.
From read_file.py:
def read_file(filename):
with open(filename, "r") as file:
return [[int(x) for x in line.split(",")] for line in file.read().splitlines()]
The algorithm remains unchanged, but this time, we use a priority queue to store the nodes to be visited. Given that we are visiting nodes in order, we can terminate the algorithm as soon as we reach the target node because we know that it will not be updated again.
From solution2.py:
def dijkstra(matrix, source, target):
updated = [[float("inf") for _ in range(len(matrix[0]))] for _ in range(len(matrix))]
updated[0][0] = matrix[0][0]
queue = [(updated[0][0], source)]
while queue:
_, (i, j) = hq.heappop(queue)
if (i, j) == target:
return updated
for x, y in [(i, j + 1), (i, j - 1), (i + 1, j), (i - 1, j)]:
if 0 <= x < len(matrix) and 0 <= y < len(matrix[0]):
alt = updated[i][j] + matrix[x][y]
if alt < updated[x][y]:
updated[x][y] = alt
hq.heappush(queue, (alt, (x, y)))
return None
The last step is to return the value of the target node.
From solution2.py:
def path_sum_four_ways(filename="matrix.txt"):
matrix = read_file(filename)
return dfs(matrix, (0, 0))[-1][-1]
Solution
425185
Usage
You can download each solution and modify it as much as you like. However, please do not copy the answer to the Euler project without thinking about it first.
Contributing
You can contribute as much as you want to the project, for more information please see README.md.


